题目内容
9.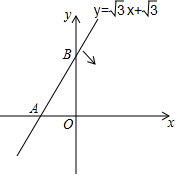 如图示直线y=$\sqrt{3}$x+$\sqrt{3}$与x轴、y轴分别交于点A、B,当直线绕着点A按顺时针方向旋转到与x轴首次重合时,点B运动的路径的长度为$\frac{2}{3}$π.
如图示直线y=$\sqrt{3}$x+$\sqrt{3}$与x轴、y轴分别交于点A、B,当直线绕着点A按顺时针方向旋转到与x轴首次重合时,点B运动的路径的长度为$\frac{2}{3}$π.
分析 先利用一次函数的解析式可确定A(-1,0),B(0,$\sqrt{3}$),再利用正切的定义求出∠BAO=60°,利用勾股定理计算出AB=2,然后根据弧长公式计算.
解答 解:当y=0时,$\sqrt{3}$x+$\sqrt{3}$=0,解得x=-1,则A(-1,0),
当x=0时,y=$\sqrt{3}$x+$\sqrt{3}$=$\sqrt{3}$,则B(0,$\sqrt{3}$),
在Rt△OAB中,∵tan∠BAO=$\frac{\sqrt{3}}{1}$=$\sqrt{3}$,
∴∠BAO=60°,
∴AB=$\sqrt{{1}^{2}+(\sqrt{3})^{2}}$=2,
∴当直线绕着点A按顺时针方向旋转到与x轴首次重合时,点B运动的路径的长度=$\frac{60•π•2}{180}$=$\frac{2}{3}$π.
故答案为$\frac{2}{3}$π.
点评 本题考查了一次函数图象与几何变换:熟练掌握旋转的性质,会计算一次函数与坐标轴的交点坐标.

练习册系列答案
 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
4.已知实数a,b满足a+1>b+1,则下列选项错误的为( )
| A. | a>b | B. | a+2>b+2 | C. | -a<-b | D. | 2a>3b |
1.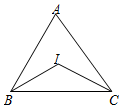 如图,在△ABC中,∠A=66°,点I是内心,则∠BIC的大小为( )
如图,在△ABC中,∠A=66°,点I是内心,则∠BIC的大小为( )
 如图,在△ABC中,∠A=66°,点I是内心,则∠BIC的大小为( )
如图,在△ABC中,∠A=66°,点I是内心,则∠BIC的大小为( )| A. | 114° | B. | 122° | C. | 123° | D. | 132° |
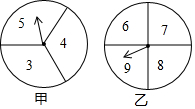 在一次数学兴趣小组活动中,李燕和刘凯两位同学设计了如图所示的两个转盘做游戏(每个转盘被分成面积相等的几个扇形,并在每个扇形区域内标上数字).游戏规则如下:两人分别同时转动甲、乙转盘,转盘停止后,若指针所指区域内两数和小于12,则李燕获胜;若指针所指区域内两数和等于12,则为平局;若指针所指区域内两数和大于12,则刘凯获胜(若指针停在等分线上,重转一次,直到指针指向某一份内为止).
在一次数学兴趣小组活动中,李燕和刘凯两位同学设计了如图所示的两个转盘做游戏(每个转盘被分成面积相等的几个扇形,并在每个扇形区域内标上数字).游戏规则如下:两人分别同时转动甲、乙转盘,转盘停止后,若指针所指区域内两数和小于12,则李燕获胜;若指针所指区域内两数和等于12,则为平局;若指针所指区域内两数和大于12,则刘凯获胜(若指针停在等分线上,重转一次,直到指针指向某一份内为止).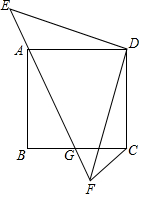 如图示,正方形ABCD的顶点A在等腰直角三角形DEF的斜边EF上,EF与BC相交于点G,连接CF.
如图示,正方形ABCD的顶点A在等腰直角三角形DEF的斜边EF上,EF与BC相交于点G,连接CF.