题目内容
6.(1)解方程:$\frac{1}{x-1}+\frac{x}{1-x}=1$(2)化简:($\frac{a}{a-b}-1$)$÷\frac{b}{{{a^2}-{b^2}}}$.
分析 (1)先去分母,再解方程即可,注意验根;
(2)先通分,再约分,根据分式的除法进行计算即可.
解答 解:(1)去分母得,1-x=x-1,
-x-x=-1-1,
-2x=-2,
x=1;
检验:把x=1代入x-1=0,
∴x=1不是原方程的解,
∴原方程无解;
(2)原式=($\frac{a}{a-b}$-$\frac{a-b}{a-b}$)•$\frac{(a+b)(a-b)}{b}$
=$\frac{a-a+b}{a-b}$•$\frac{(a+b)(a-b)}{b}$
=a+b.
点评 本题考查了分式的混合运算,以及解分式方程,通分、因式分解和约分,检验是解答的关键.

练习册系列答案
 阶梯计算系列答案
阶梯计算系列答案
相关题目
15.某种商品的进价为a元,商店将价格提高50%后作为零售价销售,在销售旺季过后,商店又以7折的价格开展促销活动,这时,一件商品的促销价格为( )
| A. | a元 | B. | 0.7a元 | C. | 1.05a元 | D. | 0.93a元 |
16.在数轴上点A表示的数是-2,点B到点A的距离是4,则点表示是( )
| A. | 6 | B. | -2 | C. | -6 | D. | -6或2 |
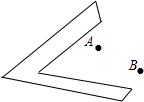 如图,在两相交公路有两村庄A、B,要修一个商店,要求到两村庄A、B的距离相等.到两公路的距离也相等.请你利用几何作图的方法,在下面的示意图中画出商店的位置.
如图,在两相交公路有两村庄A、B,要修一个商店,要求到两村庄A、B的距离相等.到两公路的距离也相等.请你利用几何作图的方法,在下面的示意图中画出商店的位置.