题目内容
13.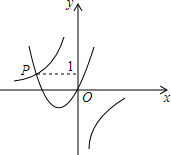 如图,已知函数y=-$\frac{3}{x}$与y=ax2+bx(a>0,b>0)的图象交于点P,点P的纵坐标为1,则关于x的方程ax2+bx+$\frac{3}{x}$=0的解是x=-3.
如图,已知函数y=-$\frac{3}{x}$与y=ax2+bx(a>0,b>0)的图象交于点P,点P的纵坐标为1,则关于x的方程ax2+bx+$\frac{3}{x}$=0的解是x=-3.
分析 根据已知函数y=-$\frac{3}{x}$与y=ax2+bx(a>0,b>0)的图象交于点P,点P的纵坐标为1,可以求得点P的坐标,将y=-$\frac{3}{x}$与y=ax2+bx联立方程组,变形可得ax2+bx+$\frac{3}{x}$=0,从而可知ax2+bx+$\frac{3}{x}$=0的解就是函数y=-$\frac{3}{x}$与y=ax2+bx(a>0,b>0)的图象交点得横坐标,本题得以解决.
解答 解:∵点P在函数y=-$\frac{3}{x}$上,点P的纵坐标为1,
∴1=$-\frac{3}{x}$,
解得x=-3,
∴函数y=-$\frac{3}{x}$与y=ax2+bx(a>0,b>0)的图象交于点P的坐标为(-3,1),
∴$\left\{\begin{array}{l}{y=-\frac{3}{x}}\\{y=a{x}^{2}+bx}\end{array}\right.$
可得,$a{x}^{2}+bx=-\frac{3}{x}$,
∴$a{x}^{2}+bx+\frac{3}{x}=0$,
解得x=-3.
故答案为:x=-3.
点评 本题考查二次函数的图象、反比例函数的图象,解题的关键是明确题意,利用数形结合的思想解答问题.

练习册系列答案
相关题目
18.下列运算正确的是( )
| A. | a2•a3=a6 | B. | a2+a2=a4 | C. | a3÷a=a | D. | (-a2)3=-a6 |
 如图,在面积为4的等边△ABC的BC边上有一点D,连接AD,以AD为边作等边△ADE,连接BE.则四边形AEBD的面积是4.
如图,在面积为4的等边△ABC的BC边上有一点D,连接AD,以AD为边作等边△ADE,连接BE.则四边形AEBD的面积是4. 小明把如图所示的平行四边形纸板挂在墙上,完飞镖游戏(每次飞镖均落在纸板上,且落在纸板的任何一个点的机会都相等),则飞镖落在阴影区域的概率是$\frac{1}{4}$.
小明把如图所示的平行四边形纸板挂在墙上,完飞镖游戏(每次飞镖均落在纸板上,且落在纸板的任何一个点的机会都相等),则飞镖落在阴影区域的概率是$\frac{1}{4}$. △ABC在平面直角坐标系中的位置如图所示,A、B、C三点在格点上,
△ABC在平面直角坐标系中的位置如图所示,A、B、C三点在格点上,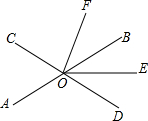 如图,直线AB,CD相交于点O,OE平分∠BOD.
如图,直线AB,CD相交于点O,OE平分∠BOD.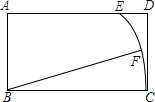 如图,在矩形ABCD中,AB=3,BC=5,以B为圆心BC为半径画弧交AD于点E,如果点F是弧EC的中点,联结FB,那么tan∠FBC的值为$\frac{1}{3}$.
如图,在矩形ABCD中,AB=3,BC=5,以B为圆心BC为半径画弧交AD于点E,如果点F是弧EC的中点,联结FB,那么tan∠FBC的值为$\frac{1}{3}$.