题目内容
8. 小明把如图所示的平行四边形纸板挂在墙上,完飞镖游戏(每次飞镖均落在纸板上,且落在纸板的任何一个点的机会都相等),则飞镖落在阴影区域的概率是$\frac{1}{4}$.
小明把如图所示的平行四边形纸板挂在墙上,完飞镖游戏(每次飞镖均落在纸板上,且落在纸板的任何一个点的机会都相等),则飞镖落在阴影区域的概率是$\frac{1}{4}$.
分析 先根据平行四边形的性质求出平行四边形对角线所分的四个三角形面积相等,再求出S1=S2即可.
解答  解:根据平行四边形的性质可得:平行四边形的对角线把平行四边形分成的四个面积相等的三角形,
解:根据平行四边形的性质可得:平行四边形的对角线把平行四边形分成的四个面积相等的三角形,
根据平行线的性质可得S1=S2,
则阴影部分的面积占$\frac{1}{4}$,
则飞镖落在阴影区域的概率是$\frac{1}{4}$.
故答案为:$\frac{1}{4}$.
点评 此题主要考查了几何概率,以及中心对称图形,用到的知识点为:概率=相应的面积与总面积之比,关键是根据平行线的性质求出阴影部分的面积与总面积的比.

练习册系列答案
相关题目
19.下面计算正确的是( )
| A. | $\sqrt{3}$+$\sqrt{5}$=$\sqrt{8}$ | B. | $\sqrt{2}$×$\sqrt{3}$=$\sqrt{6}$ | C. | $\sqrt{(-3)^{2}}$=-3 | D. | $\sqrt{7}$-$\sqrt{5}$=$\sqrt{2}$ |
16.如图,将一副三角尺按不同位置摆放,∠α与∠β互余的是( )
| A. |  | B. |  | ||
| C. |  | D. |  |
17.下列各组中,不是同类项的是( )
| A. | 32与23 | B. | -3ab与ba | C. | 0.2a2b与$\frac{1}{5}{a^2}b$ | D. | a2b3与-a3b2 |
 如图,AB=AC,AD=AE,∠BAC=∠DAE,∠1=24°,∠2=30°,∠3=54°°.
如图,AB=AC,AD=AE,∠BAC=∠DAE,∠1=24°,∠2=30°,∠3=54°°. 已知:直线AB、CD相交于O,∠1=40°,∠BOE与∠BOC互补,OM平分∠BOE,且∠CON:∠NOM=2:3,求∠COM和∠NOE的度数.
已知:直线AB、CD相交于O,∠1=40°,∠BOE与∠BOC互补,OM平分∠BOE,且∠CON:∠NOM=2:3,求∠COM和∠NOE的度数.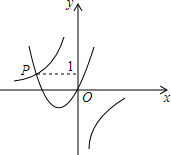 如图,已知函数y=-$\frac{3}{x}$与y=ax2+bx(a>0,b>0)的图象交于点P,点P的纵坐标为1,则关于x的方程ax2+bx+$\frac{3}{x}$=0的解是x=-3.
如图,已知函数y=-$\frac{3}{x}$与y=ax2+bx(a>0,b>0)的图象交于点P,点P的纵坐标为1,则关于x的方程ax2+bx+$\frac{3}{x}$=0的解是x=-3. 2015年12月27当日上午8时42分,第一列“和谐号”动车驶入扬州火车站.已知动车的速度比普通客车的速度快70km/h,小路同学从扬州去A地游玩,本打算乘坐普通客车,需要2小时才能到达;由于得知开通了动车,决定乘坐动车,她发现乘坐动车比乘坐普通客车节约40分钟.求动车的速度和扬州与A地之间的距离.
2015年12月27当日上午8时42分,第一列“和谐号”动车驶入扬州火车站.已知动车的速度比普通客车的速度快70km/h,小路同学从扬州去A地游玩,本打算乘坐普通客车,需要2小时才能到达;由于得知开通了动车,决定乘坐动车,她发现乘坐动车比乘坐普通客车节约40分钟.求动车的速度和扬州与A地之间的距离.