题目内容
3.我们知道:任意一个有理数与无理数的和为无理数,任意一个不为零的有理数与一个无理数的积为无理数,而零与无理数的积为零.由此可得:如果ax+b=0,其中a、b为有理数,x为无理数,那么a=0且b=0.运用上述知识,解决下列问题:
(1)如果(a+2)$\sqrt{2}$-b+3=0,其中a、b为有理数,那么a=-2,b=3;
(2)如果2b-a-(a+b-4)$\sqrt{3}$=5,其中a、b为有理数,求3a+2b的平方根.
分析 (1)根据a,b为有理数,由已知等式求出a与b的值即可;
(2)已知等式右边化为0,根据a,b为有理数,求出a与b的值,即可确定出3a+2b的平方根.
解答 解:(1)由(a+2)$\sqrt{2}$-b+3=0,得到a+2=0,-b+3=0,
解得:a=-2,b=3;
(2)已知等式整理得:2b-a-(a+b-4)$\sqrt{3}$-5=0,
∴$\left\{\begin{array}{l}a+b-4=0\\ 2b-a-5=0\end{array}\right.$,
解得:$\left\{\begin{array}{l}a=1\\ b=3\end{array}\right.$,
则3a+2b=9,9的平方根为±3.
故答案为:(1)-2;3
点评 此题考查了实数的运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
13. 如图,在长方形ABCD中,E是CD中点,连结AE并延长交BC的延长线于点F,连结BD,DF,下列结论:①△ADE≌△CEF;②∠AFD+∠BDC=∠BAF;③3DG=DF;④BD⊥DF,其中正确的是( )
如图,在长方形ABCD中,E是CD中点,连结AE并延长交BC的延长线于点F,连结BD,DF,下列结论:①△ADE≌△CEF;②∠AFD+∠BDC=∠BAF;③3DG=DF;④BD⊥DF,其中正确的是( )
 如图,在长方形ABCD中,E是CD中点,连结AE并延长交BC的延长线于点F,连结BD,DF,下列结论:①△ADE≌△CEF;②∠AFD+∠BDC=∠BAF;③3DG=DF;④BD⊥DF,其中正确的是( )
如图,在长方形ABCD中,E是CD中点,连结AE并延长交BC的延长线于点F,连结BD,DF,下列结论:①△ADE≌△CEF;②∠AFD+∠BDC=∠BAF;③3DG=DF;④BD⊥DF,其中正确的是( )| A. | ①②③ | B. | ①③④ | C. | ①②④ | D. | ①②③④ |
14. 如图,四边形ABCD内接于⊙O,若∠ABC=40°,则∠ADC的度数是( )
如图,四边形ABCD内接于⊙O,若∠ABC=40°,则∠ADC的度数是( )
 如图,四边形ABCD内接于⊙O,若∠ABC=40°,则∠ADC的度数是( )
如图,四边形ABCD内接于⊙O,若∠ABC=40°,则∠ADC的度数是( )| A. | 90° | B. | 100° | C. | 120° | D. | 140° |
11.下列给出的三条线段的长,其中能组成直角三角形的是( )
| A. | 62、82、102 | B. | 6、8、9 | C. | 2、$\sqrt{3}$、$\sqrt{5}$ | D. | $\sqrt{2}$、$\sqrt{3}$、$\sqrt{5}$ |
8.下列长度的三根木棒能组成三角形的是( )
| A. | 3,4,8 | B. | 4,4,8 | C. | 5,6,10 | D. | 6,7,14 |
 如图,AB=AC,AD=AE,∠BAC=∠DAE,∠1=24°,∠2=30°,∠3=54°°.
如图,AB=AC,AD=AE,∠BAC=∠DAE,∠1=24°,∠2=30°,∠3=54°°.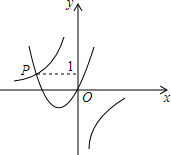 如图,已知函数y=-$\frac{3}{x}$与y=ax2+bx(a>0,b>0)的图象交于点P,点P的纵坐标为1,则关于x的方程ax2+bx+$\frac{3}{x}$=0的解是x=-3.
如图,已知函数y=-$\frac{3}{x}$与y=ax2+bx(a>0,b>0)的图象交于点P,点P的纵坐标为1,则关于x的方程ax2+bx+$\frac{3}{x}$=0的解是x=-3.