题目内容
 如图,点A、O、B是在同一直线上,OD平分∠BOC,OE平分∠AOC,则下列说法中错误的是( )
如图,点A、O、B是在同一直线上,OD平分∠BOC,OE平分∠AOC,则下列说法中错误的是( )| A、∠DOE是直角 |
| B、∠DOC与∠AOE互余 |
| C、∠AOE和∠BOD互余 |
| D、∠AOD与∠DOC互余 |
考点:余角和补角
专题:
分析:根据角平分线的性质,可得∠AOE=∠COE,∠COD=∠BOD,再根据余角和补角的定义求解即可.
解答:解:∵OD是∠BOC的平分线,OE是∠AOC平分线,
∴∠AOE=∠COE=
∠AOC,∠COD=∠BOD=
∠BOC,
∵∠AOC+∠COB=180°,
∴∠COE+∠COD=90°,
A、∠DOE为直角,正确;
B、∠DOC与∠AOE互余,正确;
C、∠AOE和∠BOD互余,正确;
D、∠AOD与∠DOC互补,原说法错误,故本选项正确.
故选D.
∴∠AOE=∠COE=
| 1 |
| 2 |
| 1 |
| 2 |
∵∠AOC+∠COB=180°,
∴∠COE+∠COD=90°,
A、∠DOE为直角,正确;
B、∠DOC与∠AOE互余,正确;
C、∠AOE和∠BOD互余,正确;
D、∠AOD与∠DOC互补,原说法错误,故本选项正确.
故选D.
点评:本题考查了余角和补角的知识,解答本题的关键是理解余角和补角的定义,掌握角平分线的性质.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图,?ABCD中,∠ABD=50°,AF⊥BC于F,AF交BD于E,点O是DE的中点,连接OA,若DE=2AB,则∠ADB的大小是( )
如图,?ABCD中,∠ABD=50°,AF⊥BC于F,AF交BD于E,点O是DE的中点,连接OA,若DE=2AB,则∠ADB的大小是( )| A、25° | B、30° |
| C、20° | D、35° |
某公司在甲、乙两地同时销售某种品牌的汽车.已知在甲、乙两地的销售利润y(单位:万元)与销售量x(单位:辆)之间分别满足:y1=-x2+10x,y2=2x,若该公司在甲,乙两地共销售15辆该品牌的汽车,则能获得的最大利润为( )
| A、30万元 | B、40万元 |
| C、45万元 | D、46万元 |
用半径为12cm,圆心角为90°的扇形纸片,围成一个圆锥的侧面,这个圆锥的底面半径为( )
| A、12cm | B、6cm |
| C、3cm | D、1.5cm |
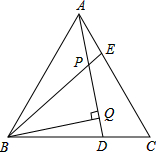 已知,如图,△ABC是等边三角形,AE=CD,BQ⊥AD于Q,BE交AD于点P,
已知,如图,△ABC是等边三角形,AE=CD,BQ⊥AD于Q,BE交AD于点P,