题目内容
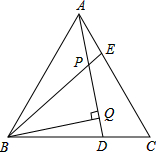 已知,如图,△ABC是等边三角形,AE=CD,BQ⊥AD于Q,BE交AD于点P,
已知,如图,△ABC是等边三角形,AE=CD,BQ⊥AD于Q,BE交AD于点P,求证:BP=2PQ.
考点:全等三角形的判定与性质,等边三角形的性质,含30度角的直角三角形
专题:证明题
分析:根据等边三角形的性质可得AB=AC,∠BAE=∠C=60°,再利用“边角边”证明△ABE和△CAD全等,根据全等三角形对应角相等可得∠1=∠2,然后求出∠BPQ=60°,再根据直角三角形两锐角互余求出∠PBQ=30°,然后根据直角三角形30°角所对的直角边等于斜边的一半证明即可.
解答: 证明:∵△ABC是等边三角形,
证明:∵△ABC是等边三角形,
∴AB=AC,∠BAE=∠C=60°,
在△ABE和△CAD中,
,
∴△ABE≌△CAD(SAS),
∴∠1=∠2,
∴∠BPQ=∠2+∠3=∠1+∠3=∠BAC=60°,
∵BQ⊥AD,
∴∠PBQ=90°-∠BPQ=90°-60°=30°,
∴BP=2PQ.
 证明:∵△ABC是等边三角形,
证明:∵△ABC是等边三角形,∴AB=AC,∠BAE=∠C=60°,
在△ABE和△CAD中,
|
∴△ABE≌△CAD(SAS),
∴∠1=∠2,
∴∠BPQ=∠2+∠3=∠1+∠3=∠BAC=60°,
∵BQ⊥AD,
∴∠PBQ=90°-∠BPQ=90°-60°=30°,
∴BP=2PQ.
点评:本题考查了全等三角形的判定与性质,等边三角形的性质,直角三角形30°角所对的直角边等于斜边的一半的性质,熟记各性质并准确识图求出△BPQ是含30°角的直角三角形是解题的关键.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
 如图所示的物体由两个紧靠在一起的圆柱组成,则俯视图应该是( )
如图所示的物体由两个紧靠在一起的圆柱组成,则俯视图应该是( )| A、两个相交的圆 |
| B、两个内切的圆 |
| C、两个外切的圆 |
| D、两个外离的圆 |
 如图,点A、O、B是在同一直线上,OD平分∠BOC,OE平分∠AOC,则下列说法中错误的是( )
如图,点A、O、B是在同一直线上,OD平分∠BOC,OE平分∠AOC,则下列说法中错误的是( )| A、∠DOE是直角 |
| B、∠DOC与∠AOE互余 |
| C、∠AOE和∠BOD互余 |
| D、∠AOD与∠DOC互余 |
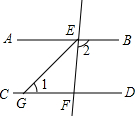 如图,AB∥CD,直线EF分别交AB、CD于点E、F,EG平分∠AEF,∠2=110°,求∠1的度数.
如图,AB∥CD,直线EF分别交AB、CD于点E、F,EG平分∠AEF,∠2=110°,求∠1的度数.