题目内容
19. (1)解不等式:$\frac{x}{2}$-$\frac{x-2}{6}$≤x-1,并把解集在数轴上表示出来.
(1)解不等式:$\frac{x}{2}$-$\frac{x-2}{6}$≤x-1,并把解集在数轴上表示出来.(2)解方程组$\left\{\begin{array}{l}{3x-y=5①}\\{3x-5y=-7②}\end{array}\right.$.
分析 (1)根据解一元一次不等式的步骤,求出不等式的解集,并把解集在数轴上表示出来即可;
(2)这两个方程未知数x的系数相同,直接选择相减便可求解.
解答 解:(1)不等式两边同时乘于6,得3x-(x-2)≤6x-6,
移项并合并,得-4x≤-8,
系数化为1,得x≥2.
故不等式的解集在数轴上表示如图所示:
(2)$\left\{\begin{array}{l}{3x-y=5①}\\{3x-5y=-7②}\end{array}\right.$,
①-②得 4y=12,
解得y=3.
把y=3代入①,得3x-3=5,解得x=$\frac{8}{3}$.
所以这个方程组的解是$\left\{\begin{array}{l}{x=\frac{8}{3}}\\{y=3}\end{array}\right.$.
点评 此题考查了一元一次不等式,要掌握解一元一次不等式的步骤,会将解集在数轴上表示出来,注意x≥2要用实心的圆点.同时考查了解二元一次方程组,若两方程两个未知数的系数相等或互为相反数时,可以直接将两个方程组相加减.

练习册系列答案
相关题目
9.某市一周空气质量报告某项污染指数的数据是:31,35,31,33,30,33,31.则对于这列数据表述正确的是( )
| A. | 众数是30 | B. | 中位数是31 | C. | 平均数是33 | D. | 极差是35 |
10.下列命题中逆命题错误的是( )
| A. | 内错角相等两直线平行 | B. | 直角三角形的两锐角互余 | ||
| C. | 全等三角形的对应边相等 | D. | 互为相反数的两个数的绝对值相等 |
7.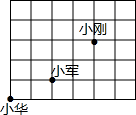 课间操时,小华、小军、小刚的位置如图所示,小军对小刚说,如果我的位置用(-1,0)表示,小华的位置用(-3,-1)表示,那么你的位置可以表示成( )
课间操时,小华、小军、小刚的位置如图所示,小军对小刚说,如果我的位置用(-1,0)表示,小华的位置用(-3,-1)表示,那么你的位置可以表示成( )
 课间操时,小华、小军、小刚的位置如图所示,小军对小刚说,如果我的位置用(-1,0)表示,小华的位置用(-3,-1)表示,那么你的位置可以表示成( )
课间操时,小华、小军、小刚的位置如图所示,小军对小刚说,如果我的位置用(-1,0)表示,小华的位置用(-3,-1)表示,那么你的位置可以表示成( )| A. | (1,2) | B. | (1,3) | C. | (0,2) | D. | (2,2) |
4.直线l是以二元一次方程8x-4y=5的解为坐标所构成的直线,则该直线不经过的象限是( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
9. 如图在△ABC中,AB=AC=5,BC=6,点E,F是中线AD上的两点,则图中阴影部分的面积是( )
如图在△ABC中,AB=AC=5,BC=6,点E,F是中线AD上的两点,则图中阴影部分的面积是( )
 如图在△ABC中,AB=AC=5,BC=6,点E,F是中线AD上的两点,则图中阴影部分的面积是( )
如图在△ABC中,AB=AC=5,BC=6,点E,F是中线AD上的两点,则图中阴影部分的面积是( )| A. | 30 | B. | 12 | C. | 24 | D. | 6 |