题目内容
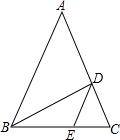
9. 如图在△ABC中,AB=AC=5,BC=6,点E,F是中线AD上的两点,则图中阴影部分的面积是( )
如图在△ABC中,AB=AC=5,BC=6,点E,F是中线AD上的两点,则图中阴影部分的面积是( )| A. | 30 | B. | 12 | C. | 24 | D. | 6 |
分析 由图形知,本图是轴对称图形,对称轴是AD所在的直线.所以阴影部分的面积为全面积的一半,由轴对称图形的性质知,BD=$\frac{1}{2}$BC=3,AD是三角形的高,AD=4,S△ABC=12,从而得到阴影部分的面积为6.
解答 解:∵AB=AC
∵△ABC是等腰三角形
AD为等腰三角形的中线
∴AD⊥BC
∴△ABD、△ACD关于AD对称,△BEF与△CEF关于AD对称
∵AB=AC,AD=$\sqrt{A{B}^{2}-B{D}^{2}}$=$\sqrt{{5}^{2}-{3}^{2}}$=4
∴S△DFB=S△DFC,S△EBF=S△ECF,S△BE=S△ACE
∴S阴=$\frac{1}{2}$S△ABC=$\frac{1}{2}$×BC×AD=$\frac{1}{2}$=6.
故选D.
点评 本题通过观察可以发现是轴对称图形,且阴影部分的面积为全面积的一半,根据轴对称图形的性质求解.其中看出三角形BEF与三角形CEF关于AD对称,面积相等是解决本题的关键.

练习册系列答案
相关题目
17.下列条件中,能够判定四边形ABCD是平行四边形的是( )
| A. | ∠A=∠C | B. | 对角线AC与BD互相平分 | ||
| C. | AB=CD | D. | 对角线AC与BD互相垂直 |
4.某校广播站招聘一名小记者,小明,小凯,小萍和小芳报名参加了三项测试,成绩如表( )
若把采访写作、计算机操作、创意设计的得分按5:2:3的比例计算三人的最后得分,那么最后得分最高的是( )
| 采访写作 | 计算机操作 | 创意设计 | |
| 小明 | 70 | 60 | 86 |
| 小凯 | 90 | 75 | 51 |
| 小萍 | 60 | 88 | 68 |
| 小芳 | 80 | 70 | 66 |
| A. | 小明 | B. | 小凯 | C. | 小萍 | D. | 小芳 |
1. 如图,在△ABC中,AB=AC,∠A=36°,BD平分∠ABC交AC于点D,过点D作DE∥AB,交BC于点E,下列结论中错误的是( )
如图,在△ABC中,AB=AC,∠A=36°,BD平分∠ABC交AC于点D,过点D作DE∥AB,交BC于点E,下列结论中错误的是( )
 如图,在△ABC中,AB=AC,∠A=36°,BD平分∠ABC交AC于点D,过点D作DE∥AB,交BC于点E,下列结论中错误的是( )
如图,在△ABC中,AB=AC,∠A=36°,BD平分∠ABC交AC于点D,过点D作DE∥AB,交BC于点E,下列结论中错误的是( )| A. | DE平分∠BDC | B. | △ABC∽△BDC∽△DEC | C. | $\frac{AD}{AB}$=$\frac{\sqrt{5}-1}{2}$ | D. | $\frac{{S}_{△BCD}}{{S}_{△ABD}}$=$\frac{1}{2}$ |
18.在0,π,$\frac{2}{3}$,$\sqrt{2}$,-$\sqrt{9}$中,无理数的个数是( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
 (1)解不等式:$\frac{x}{2}$-$\frac{x-2}{6}$≤x-1,并把解集在数轴上表示出来.
(1)解不等式:$\frac{x}{2}$-$\frac{x-2}{6}$≤x-1,并把解集在数轴上表示出来. 如图,方格中的点A,B称为格点(格线的交点),以AB为一边画△ABC,其中是直角三角形的格点C的个数为( )
如图,方格中的点A,B称为格点(格线的交点),以AB为一边画△ABC,其中是直角三角形的格点C的个数为( )