题目内容
4. 某城区为了改善全区中、小学办学条件,去年分三批为学校配备了教学器材,其中第三批共投入经费144000元.采购了电子白板16块和投影机8台.已知1块电子白板的单价比1台投影机的多3000元.
某城区为了改善全区中、小学办学条件,去年分三批为学校配备了教学器材,其中第三批共投入经费144000元.采购了电子白板16块和投影机8台.已知1块电子白板的单价比1台投影机的多3000元.(1)求购买1块电子白板和一台投影机各需多少元?
(2)已知该区去年第一批教学器材投入经费为100000元,后续两批经费的增长率相同,试求该区去年教学器材投入的经费总额.
分析 (1)可设购买1块电子白板需x元,购买一台投影机需y元,根据等量关系:①其中第三批共投入经费144000元.采购了电子白板16块和投影机8台;②已知1块电子白板的单价比1台投影机的多3000元;列出方程组求解即可;
(2)可设增长率为z,根据等量关系为:第一批教学器材投入经费×(1+增长率)2=第三批教学器材投入经费,把相关数值代入计算求得合适解即可.
解答 解:(1)设购买1块电子白板需x元,购买一台投影机需y元,依题意有
$\left\{\begin{array}{l}{16x+8y=144000}\\{x-y=3000}\end{array}\right.$,
解得$\left\{\begin{array}{l}{x=7000}\\{y=4000}\end{array}\right.$.
答:购买1块电子白板需7000元,购买一台投影机需4000元;
(2)可设增长率为z,依题意有
100000(1+z)2=144000,
(1+z)2=1.44,
∵1+z>0,
∴1+z=1.2,
∴z=20%.
100000+100000×(1+20%)+144000
=100000+120000+144000
=364000(元).
答:该区去年教学器材投入的经费总额是364000元.
点评 考查了二元一次方程组的应用,分析题意,找到关键描述语,找到合适的等量关系是解决问题的关键;同时考查了一元二次方程的应用;求平均变化率的方法为:若设变化前的量为a,变化后的量为b,平均变化率为x,则经过两次变化后的数量关系为a(1±x)2=b.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
14.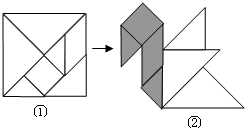 用正方形纸板制成一副七巧板,如图①,将它拼成“小天鹅”图案,如图②,若其中阴影部分的面积为6,则正方形纸板的面积为( )
用正方形纸板制成一副七巧板,如图①,将它拼成“小天鹅”图案,如图②,若其中阴影部分的面积为6,则正方形纸板的面积为( )
 用正方形纸板制成一副七巧板,如图①,将它拼成“小天鹅”图案,如图②,若其中阴影部分的面积为6,则正方形纸板的面积为( )
用正方形纸板制成一副七巧板,如图①,将它拼成“小天鹅”图案,如图②,若其中阴影部分的面积为6,则正方形纸板的面积为( )| A. | 12 | B. | 16 | C. | 18 | D. | 25 |
15.已知,△ABC∽△DEF,△ABC与△DEF的面积之比为1:2,当BC=1,对应边EF的长是( )
| A. | $\sqrt{2}$ | B. | 2 | C. | 3 | D. | 4 |
12.某区计划从甲、乙、丙、丁四支代表队中推选一支参加市级汉字听写,为此,该区组织了五轮选拔赛,在这五轮选拔赛中,甲、乙、丙、丁四支代表队的平均分都是95分,而方差依次为s甲2=0.2,s乙2=0.8,s丙2=1.6,s丁2=1.2.根据以上数据,这四支代表队中成绩最稳定的是( )
| A. | 甲代表队 | B. | 乙代表队 | C. | 丙代表队 | D. | 丁代表队 |
9.若某反比例函数y=$\frac{k}{x}$的图象经过点(3,-4),则该函数图象位于( )
| A. | 第一、二象限 | B. | 第二、四象限 | C. | 第一、三象限 | D. | 第三、四象限 |
14.下列计算正确的是( )
| A. | x2•x3=x3 | B. | (mn)2=mn2 | C. | (-x5)4=x20 | D. | (a2)3=a5 |
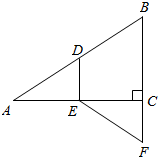 如图,在Rt△ABC中,∠ACB=90°,点D,E分别是边AB,AC的中点,延长BC到点F,使CF=$\frac{1}{2}$BC.若AB=12,求EF的长.
如图,在Rt△ABC中,∠ACB=90°,点D,E分别是边AB,AC的中点,延长BC到点F,使CF=$\frac{1}{2}$BC.若AB=12,求EF的长.