题目内容
11.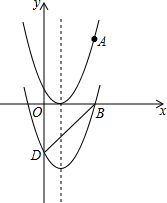 如图,抛物线C1:y=a(x-1)2经过点A(3,4).
如图,抛物线C1:y=a(x-1)2经过点A(3,4).(1)求a的值;
(2)将抛物线C1向下平移k(k>0)个单位后,得到抛物线C2,且C2经过点B(3,0),求k的值及C2的解析式;
(3)设抛物线C2角y轴于点D,点P是抛物线C2的对称轴上一点,且△PBD为直角三角形,求P点的坐标.
分析 (1)根据已知点的坐标代入已知的函数的解析式即可利用待定系数法确定二次函数的解析式;
(2)首先根据平移确定平移后的函数的解析式,然后确定抛物线C2的顶点坐标;结合图形确定n的取值范围即可.
(3)设出点P的坐标,表示出PB2,PD2,BD2,分三种情况用勾股定理计算即可.
解答 解:(1)∵抛物线C1:y=a(x-1)2经过点A(3,4).
∴4=a(3-1)2,
解得a=1,
(2)抛物线C1向下平移k(k>0)个单位后,得到抛物线C2,为y=(x-1)2-k,
∵C2经过点B(3,0),
∴0=(3-1)2-k,
解得:k=4,
∴C2的解析式为y=(x-1)2-4;
(3)由(2)可知,抛物线的解析式为y=(x-1)2-4,
∴抛物线的对称轴为x=1,
设点P(1,m),
令x=0,则y=-3,
∴D(0,-3),
∵B(3,0),
∴PB2=4+m2,PD2=1+(m+3)2,BD2=32+32=18,
∵△PBC为直角三角形,
①当∠DPB=90°时,
∴PB2+PD2=BD2,
∴4+m2+1+(m+3)2=18,
∴m1=1,m2=-2,
∴P(1,1),或P(1,-2),
②当∠PBD=90°时,
∴PB2+BD2=PD2,
∴18+4+m2=1+(m+3)2,
∴m=2,
∴P(1,2),
③当∠PDB=90°时,
∴PB2=BD2+PD2,
∴4+m2=1+(m+3)2+18,
∴m=-4,
∴P(1,-4),
∴使△PBD为直角三角形的点P坐标P(1,1)或P(1,-2)或P(1,2)或P(1,-4).
点评 本题考查了二次函数图象与几何变换,题目中还渗透了数形结合的数学思想,这也是中考中常常出现的重要的数学思想,应加强此类题目的训练.

练习册系列答案
相关题目
2.用科学记数法表示430 000是( )
| A. | 43×104 | B. | 4.3×105 | C. | 4.3×104 | D. | 4.3×106 |
6.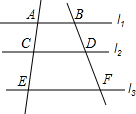 如图,已知l1∥l2∥l3,下列比例式中错误的是( )
如图,已知l1∥l2∥l3,下列比例式中错误的是( )
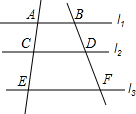 如图,已知l1∥l2∥l3,下列比例式中错误的是( )
如图,已知l1∥l2∥l3,下列比例式中错误的是( )| A. | $\frac{AC}{CE}$=$\frac{BD}{DF}$ | B. | $\frac{AC}{AE}$=$\frac{BD}{BF}$ | C. | $\frac{CE}{AE}$=$\frac{DF}{BF}$ | D. | $\frac{AE}{BF}$=$\frac{BD}{AC}$ |
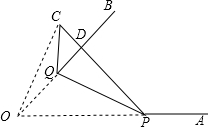 如图,∠AOB=45°,点P、Q分别是边OA、OB上的两点,且OP=2cm,将∠Q沿PQ折叠,点O落在平面内点C处,使得PQ=PD.
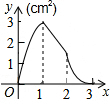
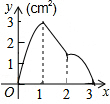
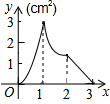
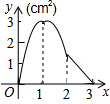
如图,∠AOB=45°,点P、Q分别是边OA、OB上的两点,且OP=2cm,将∠Q沿PQ折叠,点O落在平面内点C处,使得PQ=PD.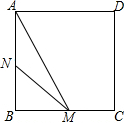 如图,正方形ABCD的边长为3cm,动点M从点B出发以3cm/s的速度沿着边BC-CD-DA运动,到达点A停止运动,另一动点N同时从点B出发,以1cm/s的速度沿着边BA向点A运动,到达点A停止运动,设点M运动时间为x(s),△AMN的面积为y(cm2),则y关于x的函数图象是( )
如图,正方形ABCD的边长为3cm,动点M从点B出发以3cm/s的速度沿着边BC-CD-DA运动,到达点A停止运动,另一动点N同时从点B出发,以1cm/s的速度沿着边BA向点A运动,到达点A停止运动,设点M运动时间为x(s),△AMN的面积为y(cm2),则y关于x的函数图象是( )