Question

9．如图，时钟的时针，分针均按时正常转动．
（1）分针每分针转动了6度，时针每分钟转动了0.5度；
（2）若现在时间恰好是2点整，求：
①经过多少分钟后，时针与分针第一次成90°角；
②从2点到4点（不含2点）有几次时针与分针成60°角，分别是几时几分？

Answer 1

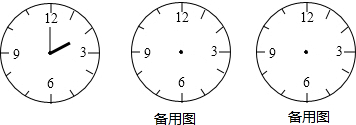
分析 （1）利用钟表表盘的特征解答．表盘共被分成60小格，每一小格所对角的度数为6°．
（2）①可设经过x分钟后，时针与分针第一次成90°角，根据角度差的等量关系列出方程求解即可；
②分三种情况：2时～3时，时针与分针成60°角；3时～4时，时针在前面，分针在后面，时针与分针成60°角；3时～4时，分针在前面，时针在后面，时针与分针成60°角；列出方程求解即可．

解答 解：（1）分针每分针转动了6度，时针每分钟转动了0.5度．
故答案为：6，0.5；
（2）①设经过x分钟后，时针与分针第一次成90°角，依题意有
6x-0.5x-60=90，
解得x=$\frac{300}{11}$．
故经过$\frac{300}{11}$分钟后，时针与分针第一次成90°角；
②2时～3时，时针与分针成60°角，
6m-60-0.5m=60，
解得m=$\frac{240}{11}$；
故3时～4时，时针在前面，分针在后面，时针与分针成60°角，
90+0.5n-6n=60，
解得n=$\frac{60}{11}$；
3时～4时，分针在前面，时针在后面，时针与分针成60°角；
6t-90-0.5t=60，
解得t=$\frac{300}{11}$．
故从2点到4点（不含2点）有3次时针与分针成60°角，分别是2时$\frac{240}{11}$分，3时$\frac{60}{11}$分，3时$\frac{300}{11}$分．

点评 本题考查了钟表问题，解题时经常用到每两个数字之间的度数是30°，分钟每分钟转过的角度为6度，时钟每分钟转过的角度为0.5度．借助图形，更容易解决．同时考查一元一次方程的应用，得到时针所走路程和分针所走路程的等量关系是解决本题的关键．