题目内容
18.(1)如图1,将一块含60°角的三角板的一边BO放在直线MN上,AB边在直线MN的上方,另一块含45°角的三角板的一边OQ在直线MN上,另一边OP在直线MN的下方,现将图1中的三角板PQO绕点O按顺时针方向旋转,当直线MN恰好为∠POQ的平分线时,如图2所示,求∠AOP的度数.(2)继续将图2中的三角板绕点O按顺时针方向旋转至图3的位置,使得边OP在∠AOB的内部,请探究∠MOQ与∠POA之间有怎样的熟练关系?并说明理由.
(3)在上述直角三角板从图1旋转至图3位置的过程中,若三角板PQO绕点O按每秒20°的速度旋转,当三角板PQO的OP边或OQ边所在直线的平分∠AOB,求此时三角板绕点O旋转的时间t的值.

分析 (1)根据三角板PQO的特性结合题意可得出∠POM=45°,在平角MON中可求出∠AOP的度数.
(2)根据角之间的关系,可用∠POA表示出∠MOQ的度数,
(3)此题分两种情况,一种OP边所在直线平分∠AOB,另一种OQ边所在直线平分∠AOB,找出两种情况下三角板PQO绕点O旋转的度数,即可求出时间t.
解答 解:(1)∵直线MN平分∠POQ,∠POQ=90°,
∴∠POM=45°,
又∵∠AOB=60°且∠MOB为平角,
∴∠POA=180°-∠POM-∠AOB=180°-45°-60°=75°,
故∠AOP的度数为75°.
(2)在三角板PQO中,∠POQ=90°-∠POA,根据题意可得:
∠MOQ=180°-60°-∠POQ=180°-60°-(90°-∠POA),
整理得:∠MOQ=∠POA+30°,
故∠MOQ与∠POA之间的关系为:∠MOQ=∠POA+30°.
(3)根据题意可知,分两种情况,
①当OP边所在直线平分∠AOB时,三角板PQO绕点O旋转的度数为360°-90°-$\frac{1}{2}$∠AOB,
∵∠AOB=60°,
∴时间t=(360°-90°-30°)÷20°=12(秒).
②当OQ边所在直线平分∠AOB时,三角板PQO绕点O旋转的度数为360°-$\frac{1}{2}$∠AOB,
∵∠AOB=60°,
∴时间t=(360°-30°)÷20°=16.5(秒).
综合①②得当OP边所在直线平分∠AOB时旋转时间为12秒,当OQ边所在直线平分∠AOB时旋转时间为16.5秒.
点评 此题考查学生角的运算能力,找对角之间的关系即可解决问题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
13. 如图,点M、N是线段AB的三等分点,则下列说法错误的是( )
如图,点M、N是线段AB的三等分点,则下列说法错误的是( )
 如图,点M、N是线段AB的三等分点,则下列说法错误的是( )
如图,点M、N是线段AB的三等分点,则下列说法错误的是( )| A. | AM=MN=NB=$\frac{1}{3}$AB | B. | 点M是线段AN的中点 | ||
| C. | 点N是线段AB的中点 | D. | AN=BM |
 如图,△ABC中,∠ACB=90°,沿CD折叠△CBD,使点B恰好落在AC边上的点E处.若∠A=24°,则∠BDC=69度.
如图,△ABC中,∠ACB=90°,沿CD折叠△CBD,使点B恰好落在AC边上的点E处.若∠A=24°,则∠BDC=69度.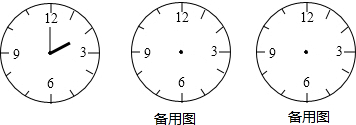
 小明从图示的二次函数y=ax2+bx+c的图象中,观察得出了下面4条信息:
小明从图示的二次函数y=ax2+bx+c的图象中,观察得出了下面4条信息: 如图,?ABCD中,AB=10cm,AD=15cm,点P在AD边上以每秒1cm的速度从点A向点D运动,点Q在BC边上,以每秒4cm的速度从点C出发,在CB间往返运动,两个点同时出发,点P到达点D时停止(同时点Q也停止运动),在运动以后,当以点P、D、Q、B为顶点组成平行四边形时,运动时间t为6或10或12秒.
如图,?ABCD中,AB=10cm,AD=15cm,点P在AD边上以每秒1cm的速度从点A向点D运动,点Q在BC边上,以每秒4cm的速度从点C出发,在CB间往返运动,两个点同时出发,点P到达点D时停止(同时点Q也停止运动),在运动以后,当以点P、D、Q、B为顶点组成平行四边形时,运动时间t为6或10或12秒.