题目内容
16.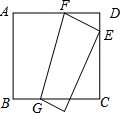 如图,将边长为12厘米的正方形ABCD折叠,使得A点落在CD上的E点,然后压平折痕FG,若FG的长为13厘米,则线段CE的长为( )
如图,将边长为12厘米的正方形ABCD折叠,使得A点落在CD上的E点,然后压平折痕FG,若FG的长为13厘米,则线段CE的长为( )| A. | 5 | B. | 6 | C. | 7 | D. | 8 |
分析 作NF⊥AD,垂足为F,连接AE,NE,利用勾股定理的知识求出FM的长,根据图形折叠前后图形不发生大小变化可得出∠DAE=∠DAE,再证明△NFM≌△ADE,得到FM=DE,从而可求得EC的长.
解答 解:作NF⊥AD,垂足为F,连接AE,NE,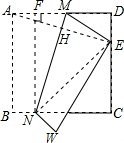
在△FMN中,由勾股定理得:FM=$\sqrt{M{N}^{2}-F{N}^{2}}$=$\sqrt{1{3}^{2}-1{2}^{2}}$=5.
∵将正方形纸片ABCD折叠,使得点A落在边CD上的E点,折痕为MN,
∴∠D=∠AHM=90°,∠DAE=∠DAE.
在△AHM和△ADE中,$\left\{\begin{array}{l}{∠D=∠AHM}\\{∠DAE=∠DAE}\end{array}\right.$,
∴△AHM∽△ADE.
∴∠AMN=∠AED.
在Rt△NFM和Rt△ADE中,$\left\{\begin{array}{l}{∠AMN=∠AED}\\{∠NFM=∠D}\\{AD=NF}\end{array}\right.$,
∴△NFM≌△ADE(AAS).
∴DE=FM=5cm.
∴EC=DC-DE=12-5=7.
故选:C.
点评 此题主要考查了图形的翻折变换,根据图形折叠前后图形不发生大小变化得出三角形的全等是解决问题的关键,难度一般.

练习册系列答案
 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案
相关题目
1.在△ABC中,已知cosB=$\frac{3}{5}$,sinC=$\frac{2}{3}$,AC=2,那么边AB等于( )
| A. | $\frac{5}{4}$ | B. | $\frac{5}{3}$ | C. | $\frac{20}{9}$ | D. | $\frac{12}{5}$ |
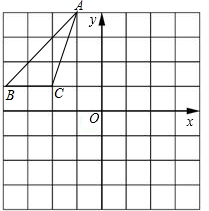 如图,在变长为1的小正方形组成的网格中,△ABC顶点均在格点上,且顶点坐标分别为A(-1,4),B(-4,1),C(-2,1);
如图,在变长为1的小正方形组成的网格中,△ABC顶点均在格点上,且顶点坐标分别为A(-1,4),B(-4,1),C(-2,1);