题目内容
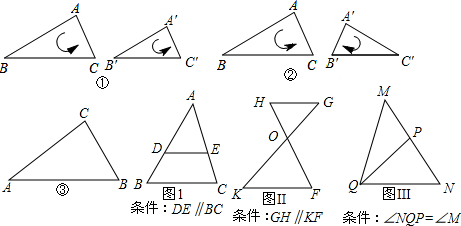
8.对于两个相似三角形,如果沿周界按对应点顺序环绕的方向相同,那么称这两个三角形互为顺相似;如果沿周界按对应点顺序环绕的方向相反,那么称这两个三角形互为逆相似.例如,如图①,△ABC∽△A′B′C′且沿周界ABCA与A′、B′、C′、A′环绕的方向相同,因此△ABC 与△A′B′C′互为顺相似;如图②,△ABC∽△A′B′C′,且沿周界ABCA与 A′、B′、C′、A′环绕的方向相反,因此△ABC 与△A′B′C′互为逆相似.(1)根据图I、图Ⅱ和图Ⅲ满足的条件,可得下列三对相似三角形:①△ADE与△ABC;②△GHO与△KFO;③△NQP与△NMQ.其中,互为顺相似的是①②;互为逆相似的是③.(填写所有符合要求的序号)
(2)如图③,在锐角△ABC中,∠A<∠B<∠C,点P在△ABC的边上(不与点A、B、C重合).过点P画直线截△ABC,使截得的一个三角形与△ABC互为逆相似.请根据点P的不同位置,探索过点P的截线的情形,画出图形并说明截线满足的条件,不必说明理由.
分析 (1)根据互为同相似和互为逆相似的定义即可作出判断;
(2)根据点P在点P在△ABC的边上(不与点A,B,C重合),需要分类讨论,逐一分析求解.
解答  解:(1)①△ADE与△ABC;②△GHO与△KFO互为顺相似;③△NQP与△NMQ互为逆相似,
解:(1)①△ADE与△ABC;②△GHO与△KFO互为顺相似;③△NQP与△NMQ互为逆相似,
故答案为:①②,③;
(2)如图1,①点P在AC(不含点A、C)上,过点B作∠CBM=∠A,BM交AC于点M.
当点P在AM(不含点M)上时,
过点P1只能画出1条截线P1Q,使∠AP1Q=∠ABC,此时△AP1Q与△ABC互为逆相似;
当点P在CM上时,过点P2只能画出2条截线P2Q1、P2Q2,
分别使∠AP2Q1=∠ABC,∠CP2Q2=∠ABC,
此时△AP2Q1、△Q2P2C都与△ABC互为逆相似.
故点P为AC边上(不与点A,C重合),
②如图2,点P在AB(不含点A、B)上,
过点C作∠BCM=∠A,CM交AB于点M,
当点P在AM(不含点M)上时,过点P1只能画出1条截线P1Q,
使∠AP1Q=∠ACB,此时△AP1Q与△ABC互为逆相似;
当点P在BM上时,过点P2只能画出2条截线P2Q1、P2Q2,
分别使∠AP2Q1=∠ACB,∠BP2Q2=∠ACB,
此时△AP2Q1、△Q2P2B都与△ABC互为逆相似.
③如图3,点P在BC(不含C、B)上,
过点P只能画出2条截线PQ1、PQ2,分别使∠CPQ1=∠CAB,∠BPQ2=∠CAB,
此时△CPQ1、△Q2PB都与△ABC互为逆相似.
点评 主要考查了相似三角形的知识点、分类讨论的数学思想以及接受与理解新生事物的能力.准确理解题设条件中“同相似”“逆相似”的定义是正确解题的先决条件,在分析与解决问题的过程中,要考虑全面,进行分类讨论,避免漏解.

练习册系列答案
相关题目
18.在平面直角坐标系中,点M(-5,-3m+4)在第三象限,则m的取值范围是( )
| A. | m<$\frac{4}{3}$ | B. | m>-$\frac{4}{3}$ | C. | m>$\frac{4}{3}$ | D. | m<-$\frac{4}{3}$ |
19.二元一次方程x-2y=4( )
| A. | 有一个解且只有一个解 | B. | 无解 | ||
| C. | 有无数多个解 | D. | 有两个解且只有两个解 |
17.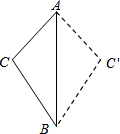 如图,将三边长分别为3、4、5的△ABC沿最长边AB翻折成△ABC′,则CC′的长为( )
如图,将三边长分别为3、4、5的△ABC沿最长边AB翻折成△ABC′,则CC′的长为( )
 如图,将三边长分别为3、4、5的△ABC沿最长边AB翻折成△ABC′,则CC′的长为( )
如图,将三边长分别为3、4、5的△ABC沿最长边AB翻折成△ABC′,则CC′的长为( )| A. | $\frac{12}{5}$ | B. | $\frac{5}{12}$ | C. | $\frac{5}{6}$ | D. | $\frac{24}{5}$ |
18.化简(1+$\frac{1}{a-1}$)÷$\frac{a}{{a}^{2}-2a+1}$的结果是( )
| A. | $\frac{a}{(a-1)^{2}}$ | B. | a-1 | C. | $\frac{1}{a}$ | D. | $\frac{a-1}{a}$ |
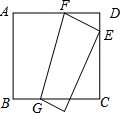 如图,将边长为12厘米的正方形ABCD折叠,使得A点落在CD上的E点,然后压平折痕FG,若FG的长为13厘米,则线段CE的长为( )
如图,将边长为12厘米的正方形ABCD折叠,使得A点落在CD上的E点,然后压平折痕FG,若FG的长为13厘米,则线段CE的长为( )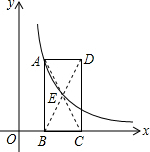 已知如图:矩形ABCD的边BC在x轴上,E为对角线AC、BD的交点,点B、D的坐标分别为B(1,0),D(3,3).
已知如图:矩形ABCD的边BC在x轴上,E为对角线AC、BD的交点,点B、D的坐标分别为B(1,0),D(3,3).
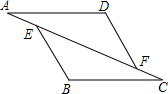 如图,△AFD和△BEC中,点A、E、F、C在同一直线上,有下面四个论断:①AD=CB;②AE=CF;③∠B=∠D;④AD∥BC.请用其中三个作为条件,余下一个作为结论,使它组成一个真命题,并加以证明.
如图,△AFD和△BEC中,点A、E、F、C在同一直线上,有下面四个论断:①AD=CB;②AE=CF;③∠B=∠D;④AD∥BC.请用其中三个作为条件,余下一个作为结论,使它组成一个真命题,并加以证明.