题目内容
5.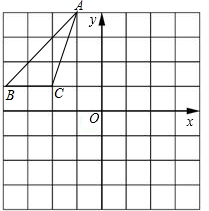 如图,在变长为1的小正方形组成的网格中,△ABC顶点均在格点上,且顶点坐标分别为A(-1,4),B(-4,1),C(-2,1);
如图,在变长为1的小正方形组成的网格中,△ABC顶点均在格点上,且顶点坐标分别为A(-1,4),B(-4,1),C(-2,1);(1)将△ABC向下平移5个单位得到△A1B1C1,请画出△A1B1C1,其中点C的对应点C1的坐标是(-2,-4);
(2)将△ABC绕点A逆时针旋转90°得△AB2C2,请画出△AB2C2,并求出旋转过程中,点C的路径长.
分析 (1)根据平移的性质画出点A、B、C平移后的对应点A1、B1、C1即可得到△A1B1C1;
(2)利用网格特点,根据旋转的性质画出点B、C旋转后的对应点B2、C2即可得到△AB2C2,由于点C变换到C2的路径是以点A为圆心、AC为半径,圆心角为90°的弧,所以根据弧长公式可计算出点C变换到C2的路径长.
解答 解:(1)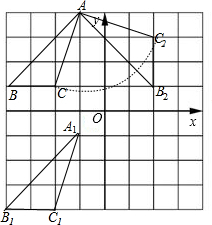 如图,△A1B1C1为所作,点C的对应点C1的坐标为(-2,-4);
如图,△A1B1C1为所作,点C的对应点C1的坐标为(-2,-4);
故答案为(-2,-4);
(2)如图,△AB2C2为所作,
AC=$\sqrt{{1}^{2}+{3}^{2}}$=$\sqrt{10}$,
所以旋转过程中点C的路径长=$\frac{90•π•\sqrt{10}}{180}$=$\frac{\sqrt{10}}{2}$π.
点评 本题考查了作图-旋转变换:根据旋转的性质可知,对应角都相等都等于旋转角,对应线段也相等,由此可以通过作相等的角,在角的边上截取相等的线段的方法,找到对应点,顺次连接得出旋转后的图形.也考查了平移变换.

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目
15.有下列四个命题:
①若两条直线被第三条直线所截,则同旁内角互补
②如果两条直线都与第三条直线平行,那么这两条直线也互相平行
③点到直线的距离是指直线外一点到这条直线的垂线段
④在同一平面内,过一点有且只有一条直线与已知直线垂直
其中真命题是( )
①若两条直线被第三条直线所截,则同旁内角互补
②如果两条直线都与第三条直线平行,那么这两条直线也互相平行
③点到直线的距离是指直线外一点到这条直线的垂线段
④在同一平面内,过一点有且只有一条直线与已知直线垂直
其中真命题是( )
| A. | ①② | B. | ②④ | C. | ②③ | D. | ③④ |
10.教材第25页有这样一段话:“一般地,如果二次函数y=ax2+bx+c的图象与x轴(注:x轴即直线y=0)有两个公共点,那么一元二次方程ax2+bx+c=0有两个不相等的实数根.”反之,利用函数的图象判断方程x2-x-6=$\frac{1}{x}$实数根的情况是( )
| A. | 有三个实数根 | B. | 有两个实数根 | C. | 有一个实数根 | D. | 无实数根 |
17.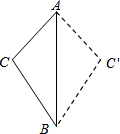 如图,将三边长分别为3、4、5的△ABC沿最长边AB翻折成△ABC′,则CC′的长为( )
如图,将三边长分别为3、4、5的△ABC沿最长边AB翻折成△ABC′,则CC′的长为( )
 如图,将三边长分别为3、4、5的△ABC沿最长边AB翻折成△ABC′,则CC′的长为( )
如图,将三边长分别为3、4、5的△ABC沿最长边AB翻折成△ABC′,则CC′的长为( )| A. | $\frac{12}{5}$ | B. | $\frac{5}{12}$ | C. | $\frac{5}{6}$ | D. | $\frac{24}{5}$ |
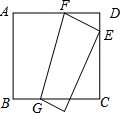 如图,将边长为12厘米的正方形ABCD折叠,使得A点落在CD上的E点,然后压平折痕FG,若FG的长为13厘米,则线段CE的长为( )
如图,将边长为12厘米的正方形ABCD折叠,使得A点落在CD上的E点,然后压平折痕FG,若FG的长为13厘米,则线段CE的长为( )
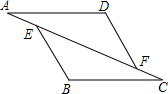 如图,△AFD和△BEC中,点A、E、F、C在同一直线上,有下面四个论断:①AD=CB;②AE=CF;③∠B=∠D;④AD∥BC.请用其中三个作为条件,余下一个作为结论,使它组成一个真命题,并加以证明.
如图,△AFD和△BEC中,点A、E、F、C在同一直线上,有下面四个论断:①AD=CB;②AE=CF;③∠B=∠D;④AD∥BC.请用其中三个作为条件,余下一个作为结论,使它组成一个真命题,并加以证明.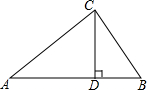 如图所示,在△ABC中,CD⊥AB于点D,若AD=2BD,AC=4,BC=3,求BD的长.
如图所示,在△ABC中,CD⊥AB于点D,若AD=2BD,AC=4,BC=3,求BD的长.