题目内容
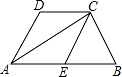
.已知:如图所示,AB∥CD,AD∥CE,且∠ACB=90°,E 为 AB 的中点.
(1)试说明 DE 与 AC 互相平分;
探究:当四边形 AECD 是正方形时,求∠B 的度数.
【考点】平行四边形的判定与性质;正方形的性质.
【分析】(1)证四边形 ADCE 是平行四边形,得出 DE 与 AC 互相平分即可; 当四边形 AECD 是正方形时,证出△BCE 是等腰 Rt△,由此可求出∠B 的度数.
【解答】(1 证明:连接 DE,
∵AB∥CD,AD∥CE,
∴四边形 AECD 是平行四边形,
∴DE 与 AC 互相平分; 解:∵四边形 AECD 是正方形,
∴CE⊥AB,AE=CE,
∵在 Rt△ACB 中,E 为 AB 的中点.
∴CE=AE=EB,

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
相关题目
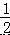 不是单项式
不是单项式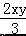 是系数为﹣
是系数为﹣ 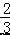 的二次单项式
的二次单项式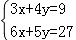 ,则 8x+8y=
,则 8x+8y=