题目内容
同一直角坐标系中,一次函数 y1=k1x+b 与正比例函数 y2=k2x 的图象如图所示,则满足 y1≥y2 的
x 取值范围是( )
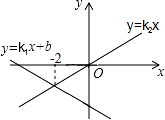
A.x≤﹣2 B.x≥﹣2 C.x<﹣2 D.x>﹣2
A
【考点】一次函数与一元一次不等式.
【分析】观察函数图象得到当 x≤﹣2 时,直线 l1:y1=k1x+b1 都在直线 l2:y2=k2x 的上方,即 y1≥y2.
【解答】解:当 x≤﹣2 时,直线 l1:y1=k1x+b1 都在直线 l2:y2=k2x 的上方,即 y1≥y2. 故选 A.
【点评】本题考查了一次函数与一元一次不等式的关系:从函数的角度看,就是寻求使一次函数 y=ax+b 的值大于(或小于)0 的自变量 x 的取值范围;从函数图象的角度看,就是确定直线 y=kx+b 在 x 轴上(或下)方部分所有的点的横坐标所构成的集合.也考查了观察函数图象的能力.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目

 经过两次下调后,决定以每平方米4860元的均价开盘销售.
经过两次下调后,决定以每平方米4860元的均价开盘销售.