题目内容
3.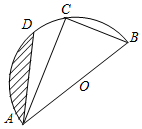 已知:如图,AB为半圆O的直径,C、D是半圆O上的两点,若直径AB的长为4,且BC=2,∠DAC=15°.
已知:如图,AB为半圆O的直径,C、D是半圆O上的两点,若直径AB的长为4,且BC=2,∠DAC=15°.(1)求∠DAB的度数;
(2)求图中阴影部分的面积(结果保留π).
分析 (1)根据含30°角的直角三角形性质求出∠CAB,即可得出答案;
(2)连接OD,求出∠DOA,分别求出扇形AOD和△AOD面积,即可得出答案.
解答 解:(1)∵AB是直径,
∴∠ACB=90°,
又∵BC=2,AB=4,
∴BC=$\frac{1}{2}$AB,
∴∠BAC=30°,
∴∠DAB=DAC+∠BAC=15°+30°=45°;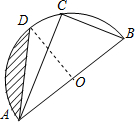 (2)连接OD,
(2)连接OD,
∵直径AB=4,
∴半径OD=OA=2,
∵OA=OD,∠DAB=45°,
∴∠ADO=∠DAB=45°,
∴∠AOD=90°,
∴阴影部分的面积S=S扇形AOD-S△AOD=$\frac{90×π×{2}^{2}}{360}$-$\frac{1}{2}$×2×2=π-2.
点评 本题考查了含30°角的直角三角形性质,扇形的面积计算,圆周角定理等知识点,能求出∠CAB=30°和∠AOD=90°是解此题的关键.

练习册系列答案
相关题目
18.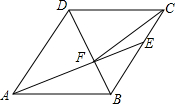 如图,在菱形ABCD中,AB=6,∠DAB=60°,AE分别交BC、BD于点E、F,若CE=2,连接CF.以下结论:①∠BAF=∠BCF;②点E到AB的距离是2$\sqrt{3}$;③S△CDF:S△BEF=9:4;④tan∠DCF=$\frac{3}{7}$.其中正确的有( )
如图,在菱形ABCD中,AB=6,∠DAB=60°,AE分别交BC、BD于点E、F,若CE=2,连接CF.以下结论:①∠BAF=∠BCF;②点E到AB的距离是2$\sqrt{3}$;③S△CDF:S△BEF=9:4;④tan∠DCF=$\frac{3}{7}$.其中正确的有( )
 如图,在菱形ABCD中,AB=6,∠DAB=60°,AE分别交BC、BD于点E、F,若CE=2,连接CF.以下结论:①∠BAF=∠BCF;②点E到AB的距离是2$\sqrt{3}$;③S△CDF:S△BEF=9:4;④tan∠DCF=$\frac{3}{7}$.其中正确的有( )
如图,在菱形ABCD中,AB=6,∠DAB=60°,AE分别交BC、BD于点E、F,若CE=2,连接CF.以下结论:①∠BAF=∠BCF;②点E到AB的距离是2$\sqrt{3}$;③S△CDF:S△BEF=9:4;④tan∠DCF=$\frac{3}{7}$.其中正确的有( )| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
15.下列图形中,是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
13. 如图,线段AB的坐标分别是A(2,4)、B(8,2),以原点O为位似中心,将线段AB缩小后得线段A′B′.若A点的对应点A′的坐标为(-1,-2),则点B的对应点B′的坐标是( )
如图,线段AB的坐标分别是A(2,4)、B(8,2),以原点O为位似中心,将线段AB缩小后得线段A′B′.若A点的对应点A′的坐标为(-1,-2),则点B的对应点B′的坐标是( )
 如图,线段AB的坐标分别是A(2,4)、B(8,2),以原点O为位似中心,将线段AB缩小后得线段A′B′.若A点的对应点A′的坐标为(-1,-2),则点B的对应点B′的坐标是( )
如图,线段AB的坐标分别是A(2,4)、B(8,2),以原点O为位似中心,将线段AB缩小后得线段A′B′.若A点的对应点A′的坐标为(-1,-2),则点B的对应点B′的坐标是( )| A. | (-4,-1) | B. | (-1,-4) | C. | (5,-4) | D. | (-5,-4) |
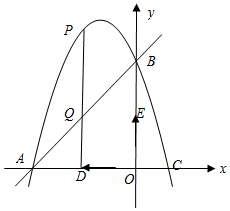 如图,抛物线经过点A(-3,0)、B(0,3),C(1,0).
如图,抛物线经过点A(-3,0)、B(0,3),C(1,0). 已知,在四边形ABCD中,AB=AD,∠B=∠D,请说明CB=CD的理由.
已知,在四边形ABCD中,AB=AD,∠B=∠D,请说明CB=CD的理由. 如图,直线a∥b,直线c与a、b均相交.如果∠1=50°,那么∠2的度数是130°.
如图,直线a∥b,直线c与a、b均相交.如果∠1=50°,那么∠2的度数是130°. 新学期伊始,学校联系厂家出售作业本,若学生在学校购买每个作业本1.5元,去校外的商店购买每个作业本2元.学校对学生一学期使用作业本的数量进行了调查,收集了30个学生一学期使用作业本的数据,整理绘制成如图的条形统计图:
新学期伊始,学校联系厂家出售作业本,若学生在学校购买每个作业本1.5元,去校外的商店购买每个作业本2元.学校对学生一学期使用作业本的数量进行了调查,收集了30个学生一学期使用作业本的数据,整理绘制成如图的条形统计图: