题目内容
8.先化简($\frac{2}{a+1}$-$\frac{2a-3}{{a}^{2}-1}$)÷$\frac{1}{a+1}$,然后在-2<a<2内选一个合适的整数代入求值.分析 直接将括号里面进行通分,进而化简,找出合适的值代入即可.
解答 解:($\frac{2}{a+1}$-$\frac{2a-3}{{a}^{2}-1}$)÷$\frac{1}{a+1}$,
=[$\frac{2(a-1)}{(a+1)(a-1)}$-$\frac{2a-3}{(a+1)(a-1)}$]×(a+1)
=$\frac{1}{(a+1)(a-1)}$×(a+1)
=$\frac{1}{a-1}$,
∵(a-1)(a+1)≠0,
∴a≠1且a≠-1,
∴当a=0时,
原式=$\frac{1}{0-1}$=-1.
点评 此题主要考查了分式的化简求值,正确进行分式的混合运算是解题关键.

练习册系列答案
相关题目
18. 如图,在Rt△ABC中,∠BAC=90°,将△ABC绕点A顺时针旋转90°后得到△AB′C′(点B的对应点是点B′,点C的对应点是点C′,连接CC′.若∠CC′B′=32°,则∠B的大小是( )
如图,在Rt△ABC中,∠BAC=90°,将△ABC绕点A顺时针旋转90°后得到△AB′C′(点B的对应点是点B′,点C的对应点是点C′,连接CC′.若∠CC′B′=32°,则∠B的大小是( )
 如图,在Rt△ABC中,∠BAC=90°,将△ABC绕点A顺时针旋转90°后得到△AB′C′(点B的对应点是点B′,点C的对应点是点C′,连接CC′.若∠CC′B′=32°,则∠B的大小是( )
如图,在Rt△ABC中,∠BAC=90°,将△ABC绕点A顺时针旋转90°后得到△AB′C′(点B的对应点是点B′,点C的对应点是点C′,连接CC′.若∠CC′B′=32°,则∠B的大小是( )| A. | 32° | B. | 64° | C. | 77° | D. | 87° |
18.如果$\sqrt{x(x-5)}$=$\sqrt{x}$•$\sqrt{x-5}$成立,则( )
| A. | x≥5 | B. | 0≤x≤5 | C. | x≥0 | D. | x为任意实数 |
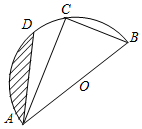 已知:如图,AB为半圆O的直径,C、D是半圆O上的两点,若直径AB的长为4,且BC=2,∠DAC=15°.
已知:如图,AB为半圆O的直径,C、D是半圆O上的两点,若直径AB的长为4,且BC=2,∠DAC=15°.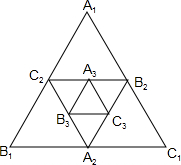 如图,小强作出边长为1的第1个等边△A1B1C1,计算器面积为S1,然后分别取△A1B1C1三边的中点A2、B2、C1,作出第2个等边△A2B2C2,计算其面积为S2,用同样的方法,作出第3个等边△A3B3C3,计算其面积为S3,按此规律进行下去,…,由此可得,第20个等边△A20B20C20的面积S20=$\frac{\sqrt{3}}{{4}^{20}}$.
如图,小强作出边长为1的第1个等边△A1B1C1,计算器面积为S1,然后分别取△A1B1C1三边的中点A2、B2、C1,作出第2个等边△A2B2C2,计算其面积为S2,用同样的方法,作出第3个等边△A3B3C3,计算其面积为S3,按此规律进行下去,…,由此可得,第20个等边△A20B20C20的面积S20=$\frac{\sqrt{3}}{{4}^{20}}$.