题目内容
18.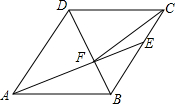 如图,在菱形ABCD中,AB=6,∠DAB=60°,AE分别交BC、BD于点E、F,若CE=2,连接CF.以下结论:①∠BAF=∠BCF;②点E到AB的距离是2$\sqrt{3}$;③S△CDF:S△BEF=9:4;④tan∠DCF=$\frac{3}{7}$.其中正确的有( )
如图,在菱形ABCD中,AB=6,∠DAB=60°,AE分别交BC、BD于点E、F,若CE=2,连接CF.以下结论:①∠BAF=∠BCF;②点E到AB的距离是2$\sqrt{3}$;③S△CDF:S△BEF=9:4;④tan∠DCF=$\frac{3}{7}$.其中正确的有( )| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
分析 证明△ABF≌△CBF,根据全等三角形的性质判断①,作EG⊥AB交AB的延长线于G,解直角三角形求出EG,判断②,根据三角形的面积公式、相似三角形的性质判断③,作FH⊥CD于H,根据正切的概念计算,判断④.
解答 解:∵四边形ABCD是菱形,
∴BA=BC,∠ABD=∠CBD,
在△ABF和△CBF中,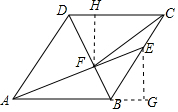
$\left\{\begin{array}{l}{BA=BC}\\{∠ABF=∠CBF}\\{BF=BF}\end{array}\right.$,
∴△ABF≌△CBF,
∴∠BAF=∠BCF,①正确;
作EG⊥AB交AB的延长线于G,
∵AD∥BC,∠DAB=60°,
∴∠EBG=60°,
∴EG=EB×sin∠EGB=2$\sqrt{3}$,②正确;
∵AB=6,CE=2,
∴S△BEF=2S△CEF,
∵AD∥BC,
∴$\frac{DF}{FB}$=$\frac{AD}{BE}$=$\frac{3}{2}$,
∴S△CFD=$\frac{3}{2}$S△CFB,
∴S△CDF:S△BEF=9:4,③正确;
作FH⊥CD于H,
则DH=$\frac{1}{2}$DF=2,FH═2$\sqrt{3}$,
∴tan∠DCF=$\frac{CH}{CH}$=$\frac{\sqrt{3}}{2}$,④错误,
故选:B.
点评 本题考查的是菱形的性质、解直角三角形的应用、相似三角形的判定和性质,掌握相似三角形的判定定理和性质定理、正确作出辅助线是解题的关键.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
8. 如图,在一个单位为1的方格纸上,△A1A2A3,△A3A4A5,△A5A6A7,…,是斜边在x轴上、斜边长分别为2,4,6,…的等腰直角三角形.若△A1A2A3的顶点坐标分别为A1(2,0),A2(1,-1),A3(0,0),则依图中所示规律,A2017的横坐标为( )
如图,在一个单位为1的方格纸上,△A1A2A3,△A3A4A5,△A5A6A7,…,是斜边在x轴上、斜边长分别为2,4,6,…的等腰直角三角形.若△A1A2A3的顶点坐标分别为A1(2,0),A2(1,-1),A3(0,0),则依图中所示规律,A2017的横坐标为( )
 如图,在一个单位为1的方格纸上,△A1A2A3,△A3A4A5,△A5A6A7,…,是斜边在x轴上、斜边长分别为2,4,6,…的等腰直角三角形.若△A1A2A3的顶点坐标分别为A1(2,0),A2(1,-1),A3(0,0),则依图中所示规律,A2017的横坐标为( )
如图,在一个单位为1的方格纸上,△A1A2A3,△A3A4A5,△A5A6A7,…,是斜边在x轴上、斜边长分别为2,4,6,…的等腰直角三角形.若△A1A2A3的顶点坐标分别为A1(2,0),A2(1,-1),A3(0,0),则依图中所示规律,A2017的横坐标为( )| A. | 1010 | B. | 2 | C. | 1 | D. | -1006 |
7.下列各运算中,计算正确的是( )
| A. | a0=1 | B. | $\sqrt{32}$-$\sqrt{8}$=2$\sqrt{2}$ | C. | $\sqrt{5}$-$\sqrt{3}$=$\sqrt{2}$ | D. | $\sqrt{18}$÷2=3 |
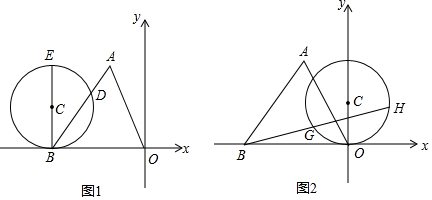
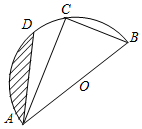 已知:如图,AB为半圆O的直径,C、D是半圆O上的两点,若直径AB的长为4,且BC=2,∠DAC=15°.
已知:如图,AB为半圆O的直径,C、D是半圆O上的两点,若直径AB的长为4,且BC=2,∠DAC=15°.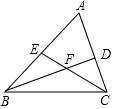 如图,在△ABC中,∠A=60°,∠ABC与∠ACB的平分线分别交AC,AB于点D,E.BD,CE相交于点F,现给出以下四个结论:①∠BFE=60°;②FE=FD;③AE=AD;④BD=BC.其中正确的是①②(把所有正确结论的序号都填在横线上)
如图,在△ABC中,∠A=60°,∠ABC与∠ACB的平分线分别交AC,AB于点D,E.BD,CE相交于点F,现给出以下四个结论:①∠BFE=60°;②FE=FD;③AE=AD;④BD=BC.其中正确的是①②(把所有正确结论的序号都填在横线上)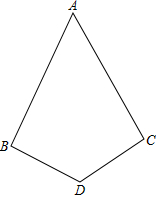 如图已知:AB=AC.DB=DC,∠ABD=∠ACD.试判断直线AD、BC的位置关系并加以证明.
如图已知:AB=AC.DB=DC,∠ABD=∠ACD.试判断直线AD、BC的位置关系并加以证明.