题目内容
14.在同一直角坐标系中.画出直线y=x+3与y=x-2的图象,并求出两条直线与x轴交点间的距离.分析 分别求得两个函数与坐标轴的交点坐标即可求得两函数的图象;分别求得两条直线与x轴的交点坐标后即可求得两条直线在x轴上截的线段的长.
解答 解:令y=0,则x+3=0,解得:x=-3,
将x=0代y=x+3得,y=3,
故y=x+3与x轴交与点(-3,0),与y轴交与点(0,3)
令y=0,则x-2=0,解得:x=-2,
将x=0代y=x-2得,y=-2,
故y=x-2与x轴交与点(2,0),与y轴交与点(0,-2)
故图象为: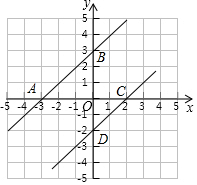
因为直线与y=x+3与x轴交与点(-3,0),直线与y=x-2与x轴交与点(2,0),
所以两条直线与x轴交点间的距离为5.
点评 本题考查了一次函数的图象和一次函数图象上点点坐标特征,解题的关键是利用两点法作出函数的图象.

练习册系列答案
相关题目
4.若x=2是关于x的方程mx+2=3(m-x)的解,则m的值是( )
| A. | 4 | B. | 6 | C. | 8 | D. | 10 |
2.若相似△ABC与△DEF的相似比为1:3,则△ABC与△DEF的周长比为( )
| A. | 1:3 | B. | 1:9 | C. | 3:1 | D. | 9:1 |
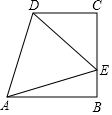 如图,在四边形ABCD中,∠B=∠C=90°,AB=BC,点E在边BC上,△ADE为等边三角形.若CD=2.求AD的长.
如图,在四边形ABCD中,∠B=∠C=90°,AB=BC,点E在边BC上,△ADE为等边三角形.若CD=2.求AD的长.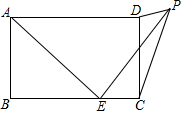 如图,在矩形ABCD中,AB=3,BC=5,点E为BC边上一个动点,连接AE,将线段AE绕点E顺时针旋转90°,点A落在点P处,当点P在矩形ABCD外部时,连接PC、PD.若△DPC为直角三角形,则BE的长为3或$\frac{5+\sqrt{17}}{2}$.
如图,在矩形ABCD中,AB=3,BC=5,点E为BC边上一个动点,连接AE,将线段AE绕点E顺时针旋转90°,点A落在点P处,当点P在矩形ABCD外部时,连接PC、PD.若△DPC为直角三角形,则BE的长为3或$\frac{5+\sqrt{17}}{2}$.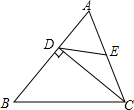 如图,△ABC中,CD⊥AB于点D,若AD=6,DE=5,AC=2DE,则CD的长等于8.
如图,△ABC中,CD⊥AB于点D,若AD=6,DE=5,AC=2DE,则CD的长等于8.