题目内容
11.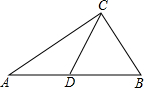 如图,在Rt△ABC中,∠ACB=90°,∠A=30°,BC=5,CD是AB边上的中线,则CD的长是5.
如图,在Rt△ABC中,∠ACB=90°,∠A=30°,BC=5,CD是AB边上的中线,则CD的长是5.
分析 先根据含30°的直角三角形的性质得出AB=10,再根据直角三角形斜边上的中线等于斜边的一半可得CD=$\frac{1}{2}$AB.
解答 解:∵在Rt△ABC中,∠ACB=90°,∠A=30°,BC=5,
∴AB=10,
∵∠ACB=90°,CD是AB边上的中线,
∴CD=$\frac{1}{2}$AB=$\frac{1}{2}$×10=5.
故答案为:5
点评 本题考查了直角三角形斜边上的中线等于斜边的一半的性质,熟记性质是解题的关键.

练习册系列答案
相关题目
1.学校为了丰富学生课余活动开展了一次“校园歌手大奖赛”的歌咏比赛,共有18名同学入围,他们的决赛成绩如下表:
则入围同学决赛成绩的中位数和众数分别是( )
| 成绩(分) | 9.40 | 9.50 | 9.60 | 9.70 | 9.80 | 9.90 |
| 人数 | 2 | 3 | 5 | 4 | 3 | 1 |
| A. | 9.70,9.60 | B. | 9.60,9.60 | C. | 9.60,9.70 | D. | 9.65,9.60 |
16.在某次数学摸底考试中有3个男同学和2个女同学获得了满分,要想从中随机挑选一个同学参加市数学竞赛,其中选中男生的概率是( )
| A. | $\frac{2}{5}$ | B. | $\frac{3}{5}$ | C. | $\frac{2}{3}$ | D. | 1 |
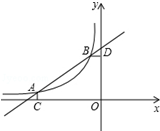 如图,已知A(-4,$\frac{1}{2}$),B(-1,a)是一次函数y=$\frac{1}{2}$x+b与反比例函数y=$\frac{m}{x}$(m≠0,m<0)图象的两个交点,AC⊥x轴于C,BD⊥y轴于D.
如图,已知A(-4,$\frac{1}{2}$),B(-1,a)是一次函数y=$\frac{1}{2}$x+b与反比例函数y=$\frac{m}{x}$(m≠0,m<0)图象的两个交点,AC⊥x轴于C,BD⊥y轴于D.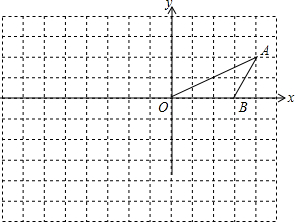 如图,O,B,A的坐标为(0,0),(3,0),(4,2).
如图,O,B,A的坐标为(0,0),(3,0),(4,2).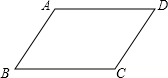 已知:如图,四边形ABCD是平行四边形.
已知:如图,四边形ABCD是平行四边形. 在Rt△ABC中,∠C=90°,AC=BC=1,将其放入平面直角坐标系,使A点与原点重合,AB在x轴上,△ABC沿x轴顺时针无滑动的滚动,点A再次落在x轴时停止滚动,则点A经过的路线与x轴围成图形的面积为π+$\frac{1}{2}$.
在Rt△ABC中,∠C=90°,AC=BC=1,将其放入平面直角坐标系,使A点与原点重合,AB在x轴上,△ABC沿x轴顺时针无滑动的滚动,点A再次落在x轴时停止滚动,则点A经过的路线与x轴围成图形的面积为π+$\frac{1}{2}$.