Question

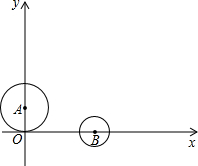如图，在直角坐标系中A（0，2），B（4，0），已知圆A的半径为2，圆B的半径为1，若圆A固定不动，圆B沿最短路线向圆A靠近使圆A与圆B相外切，求最短路线所在直线的解析式．

Answer 1

考点：圆的综合题

专题：

分析：利用最短路线所在直线的解析式为AB的解析式，设AB的解析式为y=kx+b，把（0，2）和（4，0）代入求解即可．

解答：解∵⊙B沿最短路线向⊙A靠近，应沿着连心线AB运动，
∴最短路线所在直线的解析式为AB的解析式，
设解析式为：y=kx+b把（0，2）和（4，0）代入得

2=b 0=4x+b

，解得

k=- 1 2 b=2

，
∴最短路线所在直线的解析式为y=-

1

2

x+2．

点评：本题主要考查了圆的综合题，解题的关键是明确最短路线所在直线的解析式为AB的解析式．