题目内容
 如图,一次函数y=kx+b的图象与反比例函数 y=
如图,一次函数y=kx+b的图象与反比例函数 y=| m |
| x |
(1)分别求反比例函数和一次函数的关系式;
(2)观察图象,直接写出当反比例函数值大于一次函数值时,x的取值范围.
考点:反比例函数与一次函数的交点问题
专题:
分析:(1)先把A(-2,1)代入y=
,求出m的值,得到反比例函数的解析式,再把y=-2代入y=
,求出B点坐标,然后将A、B两点的坐标代入y=kx+b,列出关于k、b的二元一次方程组,进而求出一次函数的解析式;
(2)根据图象,直接得出反比例函数值大于一次函数值的x的取值范围.
| m |
| x |
| m |
| x |
(2)根据图象,直接得出反比例函数值大于一次函数值的x的取值范围.
解答:解:(1)∵反比例函数y=
的图象过点A(-2,1),
∴1=
,解得m=-2,
∴反比例函数的解析式为y=-
.
把y=-2代入y=-
,得-2=-
,
解得x=1,
∴B(1,-2).
∵一次函数y=kx+b的图象过点A(-2,1),B(1,-2),
∴
,
解得
,
∴一次函数的解析式为:y=-x-1;
(2)由图可知,当-2<x<0或x>1时,反比例函数值大于一次函数值.
| m |
| x |
∴1=
| m |
| -2 |
∴反比例函数的解析式为y=-
| 2 |
| x |
把y=-2代入y=-
| 2 |
| x |
| 2 |
| x |
解得x=1,
∴B(1,-2).
∵一次函数y=kx+b的图象过点A(-2,1),B(1,-2),
∴
|
解得
|
∴一次函数的解析式为:y=-x-1;
(2)由图可知,当-2<x<0或x>1时,反比例函数值大于一次函数值.
点评:本题考查的是一次函数与反比例函数的交点问题,涉及到用待定系数法求一次函数及反比例函数的解析式等知识,比较简单.

练习册系列答案
 阶梯计算系列答案
阶梯计算系列答案
相关题目
 如图,AB=AC,添加下列条件,能用SAS判断△ABE≌△ACD的是( )
如图,AB=AC,添加下列条件,能用SAS判断△ABE≌△ACD的是( )| A、∠B=∠C |
| B、∠AEB=∠ADC |
| C、AE=AD |
| D、BE=DC |
 如图所示,点E、F在线段BD上,线段AC与BD互相平分,且BE=DF.求证:
如图所示,点E、F在线段BD上,线段AC与BD互相平分,且BE=DF.求证: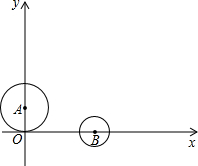 如图,在直角坐标系中A(0,2),B(4,0),已知圆A的半径为2,圆B的半径为1,若圆A固定不动,圆B沿最短路线向圆A靠近使圆A与圆B相外切,求最短路线所在直线的解析式.
如图,在直角坐标系中A(0,2),B(4,0),已知圆A的半径为2,圆B的半径为1,若圆A固定不动,圆B沿最短路线向圆A靠近使圆A与圆B相外切,求最短路线所在直线的解析式.