题目内容
已知在△ABC中，已知AB=3，AC=6，BC=7，AD是∠BAC的角平分线，求证：DC=2BD．
考点：角平分线的性质
专题：证明题
分析：作DE∥AC，得出∠EDA=∠DAC，由于AD是∠BAC的平分线，得出∠BAD=∠DAC，进而得出∠EAD=∠EDA，根据等角对等边得出EA=ED，设DE=x，则EA=x，BE=3-x，然后根据△BDE∽△BCA对应边成比例，得出
=
=
，即可求得BD的值，最后根据CD=BC-BD求得CD的值，即可证得DC=2BD．
| BD |
| BC |
| BE |
| AB |
| DE |
| AC |
解答：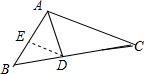
证明：作DE∥AC，
∴∠EDA=∠DAC，
∵AD是∠BAC的平分线，
∴∠BAD=∠DAC，
∴∠EAD=∠EDA，
∴EA=ED，
∵DE∥AC，
∴△BDE∽△BCA，
∴
=
=
设DE=x，则EA=x，
∴BE=3-x，
∴
=
=
，
∴x=2，
∴BD=
，
∴CD=BC-BD=7-
=
．
∴DC=2BD．
证明：作DE∥AC，∴∠EDA=∠DAC，
∵AD是∠BAC的平分线，
∴∠BAD=∠DAC，
∴∠EAD=∠EDA，
∴EA=ED，
∵DE∥AC，
∴△BDE∽△BCA，
∴
| BD |
| BC |
| BE |
| AB |
| DE |
| AC |
设DE=x，则EA=x，
∴BE=3-x，
∴
| BD |
| 7 |
| 3-x |
| 3 |
| x |
| 6 |
∴x=2，
∴BD=
| 7 |
| 3 |
∴CD=BC-BD=7-
| 7 |
| 3 |
| 14 |
| 3 |
∴DC=2BD．
点评：本题考查了角平分线的性质，平行线的性质，相似三角形的判定和性质，作出辅助线，得出DE=AE是本题的关键．
练习册系列答案
相关题目
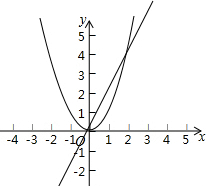如图所示，抛物线y=x2与直线y=2x在第一象限内有一个交点A．
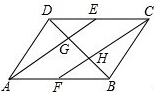如图，已知平行四边形ABCD中，点E、F分别是边DC、AB的中点，AE、CF分别与对角线BD相交于点G、H，设
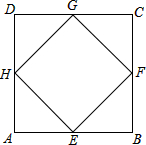（1）如图，顺次连接正方形ABCD的各边中点，得到一个小正方形EFGH．则正方形EFGH与正方形ABCD的面积比是多少？