题目内容
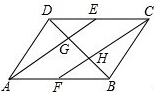 如图,已知平行四边形ABCD中,点E、F分别是边DC、AB的中点,AE、CF分别与对角线BD相交于点G、H,设
如图,已知平行四边形ABCD中,点E、F分别是边DC、AB的中点,AE、CF分别与对角线BD相交于点G、H,设| AB |
| a |
| AD |
| b |
| GE |
| CH |
| a |
| b |
考点:*平面向量
专题:
分析:求出△ABG和△EDG相似,利用相似三角形对应边成比例可得
=
,再表示出
,然后利用向量三角形法则求出
,再求解即可;同理求出
,然后求出
、
,利用向量三角形法则求出
,然后求解即可.
| EG |
| AG |
| DE |
| AB |
| DE |
| AE |
| CH |
| FH |
| CD |
| CB |
| CF |
解答:解:∵点E是CD的中点,四边形ABCD是平行四边形,
∴DE=
CD=
AB,AB∥CD,
∴△ABG∽△EDG,
∴
=
=
,
∵
=
,
∴
=
,
由向量三角形法则得,
=
+
=
+
;
∴
=
=
=
+
;
同理可得
=2,
∵
=
,
=
,
∴
=-
,
=-
,
∴
=-
,
由向量三角形法则得,
=
+
=-
-
,
∴
=
=
(-
-
)=-
-
.
∴DE=
| 1 |
| 2 |
| 1 |
| 2 |
∴△ABG∽△EDG,
∴
| EG |
| AG |
| DE |
| AB |
| 1 |
| 2 |
∵
| AB |
| a |
∴
| DE |
| 1 |
| 2 |
| a |
由向量三角形法则得,
| AE |
| AD |
| DE |
| 1 |
| 2 |
| a |
| b |
∴
| GE |
| 1 |
| 1+2 |
| AE |
| 1 |
| 3 |
| AE |
| 1 |
| 6 |
| a |
| 1 |
| 3 |
| b |
同理可得
| CH |
| FH |
∵
| AB |
| a |
| AD |
| b |
∴
| CD |
| a |
| CB |
| b |
∴
| BF |
| 1 |
| 2 |
| a |
由向量三角形法则得,
| CF |
| BF |
| CB |
| 1 |
| 2 |
| a |
| b |
∴
| CH |
| 2 |
| 1+2 |
| CF |
| 2 |
| 3 |
| 1 |
| 2 |
| a |
| b |
| 1 |
| 3 |
| a |
| 2 |
| 3 |
| b |
点评:本题考查了平面向量,平行四边形的性质,相似三角形的判定与性质,平面向量问题,熟记平行四边形法则和三角形法则是解题的关键.

练习册系列答案
相关题目
能使
有意义的实数x的值有( )
| -(x-5)2 |
| A、0个 | B、1个 | C、2个 | D、无数个 |
某班男生比女生多
,男生相当于全班人数的( )
| 3 |
| 8 |
A、
| ||
B、
| ||
C、
| ||
D、
|