Question

20．如图，直线l是一次函数y=kx+b的图象，求l与两坐标轴所围成的三角形的面积．

Answer 1

分析 由图象过点（0，1）和（3，-3）可求得函数解析式，从而可求得直线与x轴的交点，则可求得l与两坐标轴所围成的三角形的面积．

解答 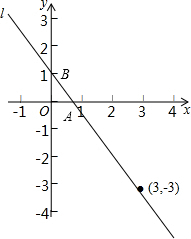解：
如图，设直线l交x轴于点A，交y轴于点B，
由图象可知函数图象过点（0，1）和（3，-3），
代入解析式可得$\left\{\begin{array}{l}{b=1}\\{3k+b=-3}\end{array}\right.$，解得$\left\{\begin{array}{l}{k=-\frac{4}{3}}\\{b=1}\end{array}\right.$，
∴直线l解析式为y=-$\frac{4}{3}$x+1，
令y=0可得0=-$\frac{4}{3}$x+1，解得x=$\frac{3}{4}$，
∴A（$\frac{3}{4}$，0），且B（0，1），
∴OA=$\frac{3}{4}$，OB=1，
∴S_△AOB=$\frac{1}{2}$OA•OB=$\frac{1}{2}$×$\frac{3}{4}$×1=$\frac{3}{8}$，
即l与两坐标轴所围成的三角形的面积为$\frac{3}{8}$．

点评 本题主要考查待定系数法，掌握函数图象上点的坐标满足函数解析式是解题的关键．