题目内容
15. 如图,△ABC中,∠BAC=90°,AD⊥BC于点D,△ABE、△ACF都是等边三角形,求证:
如图,△ABC中,∠BAC=90°,AD⊥BC于点D,△ABE、△ACF都是等边三角形,求证:(1)△ADE∽△CDF;
(2)△DEF∽△ABC.
分析 (1)利用已知和等边三角形的性质得出∠DAE=∠DCF,证出△ABC∽△DAC,得出$\frac{AB}{AD}=\frac{AC}{CD}$,证出$\frac{AE}{AD}=\frac{CF}{CD}$,即可得出结论;
(2)由相似三角形的性质得出$\frac{DE}{DF}=\frac{AD}{CD}$,∠ADE=∠CDF,得出$\frac{DE}{DF}$=$\frac{AB}{AC}$,证出∠EDF=90°=∠BAC,即可得出结论.
解答 证明:(1)∵∠BAC=90°,AD⊥BC,
∴∠ADC=90°=∠BAC,∠ABD+∠BAD=∠CAD+∠BAD=90°,
∴∠ABD=∠CAD,
∵△ABE和△ACF都是正三角形,
∴∠BAE=∠ACF=60°,AE=AB,CF=AC,
∴∠DAE=∠DCF,
∵∠ACD=∠BCA,
∴△ABC∽△DAC,
∴$\frac{AB}{AD}=\frac{AC}{CD}$,
∴$\frac{AE}{AD}=\frac{CF}{CD}$,
∴△ADE∽△CDF;
(2)∵△ADE∽△CDF,
∴$\frac{DE}{DF}=\frac{AD}{CD}$,∠ADE=∠CDF,
∴$\frac{DE}{DF}$=$\frac{AB}{AC}$,
∴∠ADE+∠ADF=∠CDF+∠ADF=90°,
即∠EDF=90°=∠BAC,
∴△DEF∽△ABC.
点评 此题主要考查了相似三角形的判定与性质、等边三角形的性质;熟练掌握等边三角形的性质,证明△ABC∽△DAC是解决问题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
3. 已知四边形ABCD各边长如图所示,且四边形OPEF≌四边形ABCD.则PE的长为( )
已知四边形ABCD各边长如图所示,且四边形OPEF≌四边形ABCD.则PE的长为( )
 已知四边形ABCD各边长如图所示,且四边形OPEF≌四边形ABCD.则PE的长为( )
已知四边形ABCD各边长如图所示,且四边形OPEF≌四边形ABCD.则PE的长为( )| A. | 3 | B. | 5 | C. | 6 | D. | 10 |
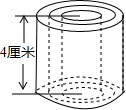 如图所示,圆柱的高是4厘米,当圆柱底面半径r(cm)变化时,圆柱的体积V(cm3)也随之变化.
如图所示,圆柱的高是4厘米,当圆柱底面半径r(cm)变化时,圆柱的体积V(cm3)也随之变化.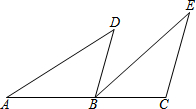 已知:如图,点A、B、C在一条直线上,BD∥CE,AB=EC,BD=CB.
已知:如图,点A、B、C在一条直线上,BD∥CE,AB=EC,BD=CB. 如图,直线l是一次函数y=kx+b的图象,求l与两坐标轴所围成的三角形的面积.
如图,直线l是一次函数y=kx+b的图象,求l与两坐标轴所围成的三角形的面积. 设二次函数y=ax2+bx+c(a≠0)图象如图所示,经过点(-1,0),试判断a、b、c、a+b+c、a-b+c、b2-4ac的符号.
设二次函数y=ax2+bx+c(a≠0)图象如图所示,经过点(-1,0),试判断a、b、c、a+b+c、a-b+c、b2-4ac的符号.