题目内容
11. 如图,AC∥DF,AC=DF,BF=EC,问线段AB与DE有怎样的关系?请说明理由.
如图,AC∥DF,AC=DF,BF=EC,问线段AB与DE有怎样的关系?请说明理由.
分析 根据平行线的性质可得∠ACB=∠DFE,根据等式的性质可得EF=BC,然后判定△ACB≌△DFE,再根据全等三角形的性质可得AB=ED,AB∥ED.
解答 解:AB=ED,AB∥ED,
理由:∵AC∥DF,
∴∠ACB=∠DFE,
∵BF=EC,
∴FB+CF=EC+FC,
即EF=BC,
在△ACB和△DFE中$\left\{\begin{array}{l}{AC=DF}\\{∠ACB=∠DFE}\\{EF=CB}\end{array}\right.$,
∴△ACB≌△DFE(SAS),
∴∠B=∠E,AB=ED,
∴AB∥ED.
点评 此题主要考查了全等三角形的判定和性质,全等三角形的判定是结合全等三角形的性质证明线段和角相等的重要工具.在判定三角形全等时,关键是选择恰当的判定条件.

练习册系列答案
 活力课时同步练习册系列答案
活力课时同步练习册系列答案 学业测评一课一测系列答案
学业测评一课一测系列答案
相关题目
3. 已知四边形ABCD各边长如图所示,且四边形OPEF≌四边形ABCD.则PE的长为( )
已知四边形ABCD各边长如图所示,且四边形OPEF≌四边形ABCD.则PE的长为( )
 已知四边形ABCD各边长如图所示,且四边形OPEF≌四边形ABCD.则PE的长为( )
已知四边形ABCD各边长如图所示,且四边形OPEF≌四边形ABCD.则PE的长为( )| A. | 3 | B. | 5 | C. | 6 | D. | 10 |
 探究:如图,已知直线l1∥l2,直线l3和直线l1、l2交于点C和点D,直线l3有一点P
探究:如图,已知直线l1∥l2,直线l3和直线l1、l2交于点C和点D,直线l3有一点P 已知,如图,在△ABC中,OB和OC分别平分∠ABC和∠ACB,过O作DE∥BC,分别交AB、AC于点D、E,若BD+CE=5,则线段DE的长为5.
已知,如图,在△ABC中,OB和OC分别平分∠ABC和∠ACB,过O作DE∥BC,分别交AB、AC于点D、E,若BD+CE=5,则线段DE的长为5. 已知:如图,BC∥EF,AD=BE,BC=EF,试证明AC=DF.
已知:如图,BC∥EF,AD=BE,BC=EF,试证明AC=DF.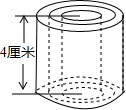 如图所示,圆柱的高是4厘米,当圆柱底面半径r(cm)变化时,圆柱的体积V(cm3)也随之变化.
如图所示,圆柱的高是4厘米,当圆柱底面半径r(cm)变化时,圆柱的体积V(cm3)也随之变化. 已知如图,点F、A、E、B在一条直线上,∠C=∠F,BC∥DE,AB=DE
已知如图,点F、A、E、B在一条直线上,∠C=∠F,BC∥DE,AB=DE 如图,直线l是一次函数y=kx+b的图象,求l与两坐标轴所围成的三角形的面积.
如图,直线l是一次函数y=kx+b的图象,求l与两坐标轴所围成的三角形的面积. 已知a,b,c代表的数在数轴上的位置如图所示,化简|a+b+c|+|a-b-c|+|c-b-a|
已知a,b,c代表的数在数轴上的位置如图所示,化简|a+b+c|+|a-b-c|+|c-b-a|