题目内容
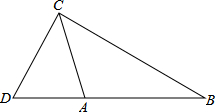如图，在△ABC中，AC=5cm，BC=8cm，△ABC的面积为12cm，点D在BA延长线上，∠DCA=∠B．（1）求△ACD的面积；
（2）比较线段CD与AB的长短．
考点：相似三角形的判定与性质
专题：常规题型
分析：（1）易证△ACD∽△DCB，可得AC：BC的值，即可解题；
（2）根据△ACD∽△DCB对应边比例等于相似比即可求得DC的值，即可解题．
（2）根据△ACD∽△DCB对应边比例等于相似比即可求得DC的值，即可解题．
解答：解：（1）∵∠DCA=∠B，∠D=∠D，
∴△ACD∽△DCB，
∴
=
=
，
∴
=
解得S△ACD=
，
（2）∵
=
=
=
，
∴BD=
AB=
AB，
∵△ADC∽△DCB
∴
=
=
=
，
∴DC=
AB＞AB．
∴△ACD∽△DCB，
∴
| S△ACD |
| S△DCB |
| S△ACD |
| S△ACD+S△ABC |
| AC2 |
| BC2 |
∴
| S△ACD |
| S△ACD+12 |
| 25 |
| 64 |
解得S△ACD=
| 100 |
| 13 |
（2）∵
| S△ACD |
| S△ABC |
| AD |
| AB |
| ||
| 12 |
| 25 |
| 39 |
∴BD=
| 25+39 |
| 39 |
| 64 |
| 39 |
∵△ADC∽△DCB
∴
| DC |
| BD |
| DC | ||
|
| AC |
| BC |
| 5 |
| 8 |
∴DC=
| 40 |
| 39 |
点评：本题考查了相似三角形的判定，考查了相似三角形对应边比例相等的性质，本题中求证△ACD∽△DCB是解题的关键．
练习册系列答案
相关题目
一种药品经过两次降价后，每盒的价格由原来的60元降到48.6元，那么平均每次降价的百分率是（ ）
| A、8.5% | B、12% |
| C、10% | D、15% |
“厚德开泰，奋发图兴”是130万泰兴人的不懈追求，130万用科学记数法表示为（ ）
| A、13×105 |
| B、1.3×106 |
| C、1.3×107 |
| D、1.3×109 |
如图，将矩形ABCD沿对角线BD折叠，使点C和点C′重合，BC′交AD于点E，若AB=4，AD=8，则DE的长为（ ）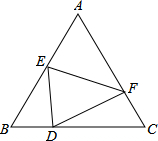
如图，已知等边△ABC，现将△ABC折叠，使A点落在BC边上D点，折痕为EF，求证：∠BED=∠FDC．计算cos80°-sin80°的值大约为（ ）
| A、0.8111 | B、-0.8111 |
| C、0.8112 |