题目内容
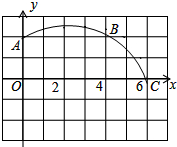 如图,在正方形网格图中建立一直角坐标系,一条圆弧经过网格点A(0,2),B(4,2)C(6,0),解答下列问题:
如图,在正方形网格图中建立一直角坐标系,一条圆弧经过网格点A(0,2),B(4,2)C(6,0),解答下列问题:(1)请在图中确定该圆弧所在圆心D点的位置,则D点坐标为
(2)连结AD,CD,求⊙D的半径(结果保留根号);
(3)求扇形DAC的面积.(结果保留π).
考点:圆的综合题
专题:
分析:(1)由圆心在AB和BC的垂直平分线上,可得出D点的位置;
(2)过点D作DE⊥y轴,交y轴于点E,在Rt△ADE中,利用勾股定理可求得AD的长,即可得出半径;
(3)连接AC,可求得AC的长,再利用勾股定理的逆定理可得∠ADC=90°,再利用扇形的面积公式求解即可.
(2)过点D作DE⊥y轴,交y轴于点E,在Rt△ADE中,利用勾股定理可求得AD的长,即可得出半径;
(3)连接AC,可求得AC的长,再利用勾股定理的逆定理可得∠ADC=90°,再利用扇形的面积公式求解即可.
解答:解:(1)如图1,作出线段AB和BC的垂直平分线的交点即为所求的D点,可知D点坐标为(2,-2),故答案为(2,-2);

(2)如图2,过点D作DE⊥y轴,交y轴于点E,在Rt△ADE中,AE=2+2=4,DE=2,由勾股定理可求得AD=2
,即⊙D的半径为2
;

(3)如图3,连接AC,在Rt△AOC中,AO=2,OC=6,由勾股定理可求得AC=2
,
在△ADC中,AD2+CD2=40=AC2,
∴∠ADC=90°,
∴S扇形ADC=
π•AD2=
×π×20=5π.


(2)如图2,过点D作DE⊥y轴,交y轴于点E,在Rt△ADE中,AE=2+2=4,DE=2,由勾股定理可求得AD=2
| 5 |
| 5 |

(3)如图3,连接AC,在Rt△AOC中,AO=2,OC=6,由勾股定理可求得AC=2
| 10 |
在△ADC中,AD2+CD2=40=AC2,
∴∠ADC=90°,
∴S扇形ADC=
| 1 |
| 4 |
| 1 |
| 4 |

点评:本题主要考查垂径定理及勾股定理、扇形的面积的综合应用,掌握圆心为三角形三边垂直平分线的交点是解决第(1)题的关键,在第(3)题中判断出△ADC为直角三角形是解题的关键.

练习册系列答案
相关题目
“厚德开泰,奋发图兴”是130万泰兴人的不懈追求,130万用科学记数法表示为( )
| A、13×105 |
| B、1.3×106 |
| C、1.3×107 |
| D、1.3×109 |
 如图,将矩形ABCD沿对角线BD折叠,使点C和点C′重合,BC′交AD于点E,若AB=4,AD=8,则DE的长为( )
如图,将矩形ABCD沿对角线BD折叠,使点C和点C′重合,BC′交AD于点E,若AB=4,AD=8,则DE的长为( )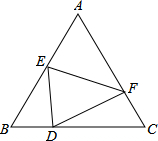 如图,已知等边△ABC,现将△ABC折叠,使A点落在BC边上D点,折痕为EF,求证:∠BED=∠FDC.
如图,已知等边△ABC,现将△ABC折叠,使A点落在BC边上D点,折痕为EF,求证:∠BED=∠FDC.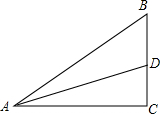 在Rt△ABC中,AD是角平分线,已知,AB=5,AC=4,BC=3,∠ACB=90°.
在Rt△ABC中,AD是角平分线,已知,AB=5,AC=4,BC=3,∠ACB=90°.