题目内容
6.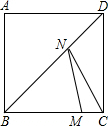 如图,正方形ABCD的边长为8,点M在BC上,且MC=2,N是BD上一动点,则NM+NC的最小值等于10.
如图,正方形ABCD的边长为8,点M在BC上,且MC=2,N是BD上一动点,则NM+NC的最小值等于10.
分析 连接AN,AC,则直线AC即为BD的垂直平分线,易知AN=NC即可推出CN+MN=AN+MN连AM交BD于点P,由点 N为BD上的动点,由三角形两边和大于第三边,知当点N运动到点P时,可得CN+MN=AP+PM=AM,CN+MN的最小值为AM的长度,由此求出AM即可解决问题.
解答 解:∵正方形是轴对称图形,点A与点C是关于直线BD为对称轴的对称点,
∴连接AN,AC,则直线AC即为BD的垂直平分线,
∴AN=NC∴CN+MN=AN+MN连AM交BD于点P,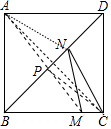
∵点 N为BD上的动点,
由三角形两边和大于第三边,
知当点N运动到点P时,
CN+MN=AP+PM=AM,CN+MN的最小值为AM的长度,
∵四边形ABCD为正方形,
∴BC=8,BM=8-2=6,∠ABM=90°,
∴AM=$\sqrt{{6}^{2}+{8}^{2}}$=10,
∴CN+MN的最小值是10.
故答案为10.
点评 本题考查了轴对称-最短路线问题,正方形的性质.此题的难点在于确定满足条件的点N的位置:利用轴对称的方法.然后熟练运用勾股定理.

练习册系列答案
相关题目
11.一组数据4,5,7,7,8,6的中位数和众数分别是( )
| A. | 7,7 | B. | 7,6.5 | C. | 6.5,7 | D. | 5.5,7 |
18.估算$\sqrt{65}$的值介于( )
| A. | 5到6之间 | B. | 6到7之间 | C. | 7到8之间 | D. | 8到9之间 |
15.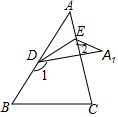 如图,△ABC中,D、E分别为AB、AC上两点,将△ABC沿直线DE折叠,使得点A落在△ABC右侧的点A1处,则∠A、∠1、∠2之间满足的关系式是( )
如图,△ABC中,D、E分别为AB、AC上两点,将△ABC沿直线DE折叠,使得点A落在△ABC右侧的点A1处,则∠A、∠1、∠2之间满足的关系式是( )
 如图,△ABC中,D、E分别为AB、AC上两点,将△ABC沿直线DE折叠,使得点A落在△ABC右侧的点A1处,则∠A、∠1、∠2之间满足的关系式是( )
如图,△ABC中,D、E分别为AB、AC上两点,将△ABC沿直线DE折叠,使得点A落在△ABC右侧的点A1处,则∠A、∠1、∠2之间满足的关系式是( )| A. | ∠A=∠1-∠2 | B. | ∠A=$\frac{1}{2}$∠1-∠2 | C. | ∠A=∠1-2∠2 | D. | 2∠A=∠1-∠2 |
16. 如图,在直角三角形ABC中,∠BAC=90°,将△ABC沿直线BC向右平移得到△DEF,连结AD、AE,则下列结论中不成立的是( )
如图,在直角三角形ABC中,∠BAC=90°,将△ABC沿直线BC向右平移得到△DEF,连结AD、AE,则下列结论中不成立的是( )
 如图,在直角三角形ABC中,∠BAC=90°,将△ABC沿直线BC向右平移得到△DEF,连结AD、AE,则下列结论中不成立的是( )
如图,在直角三角形ABC中,∠BAC=90°,将△ABC沿直线BC向右平移得到△DEF,连结AD、AE,则下列结论中不成立的是( )| A. | AD∥BE,AD=BE | B. | ∠ABE=∠DEF | ||
| C. | ED⊥AC | D. | △ADE为等边三角形 |
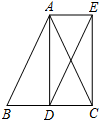 如图,在△ABC中,AB=AC,AD平分∠BAC交BC于点D,分别过点A,D作AE∥BC,DE∥AB,AE与DE相交于点E,连结CE.
如图,在△ABC中,AB=AC,AD平分∠BAC交BC于点D,分别过点A,D作AE∥BC,DE∥AB,AE与DE相交于点E,连结CE.