题目内容
15.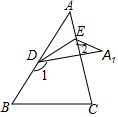 如图,△ABC中,D、E分别为AB、AC上两点,将△ABC沿直线DE折叠,使得点A落在△ABC右侧的点A1处,则∠A、∠1、∠2之间满足的关系式是( )
如图,△ABC中,D、E分别为AB、AC上两点,将△ABC沿直线DE折叠,使得点A落在△ABC右侧的点A1处,则∠A、∠1、∠2之间满足的关系式是( )| A. | ∠A=∠1-∠2 | B. | ∠A=$\frac{1}{2}$∠1-∠2 | C. | ∠A=∠1-2∠2 | D. | 2∠A=∠1-∠2 |
分析 根据图②中由于折叠∠A与∠A1是相等的,再两次运用三角形外角的性质可得结论2∠A=∠1-∠2.
解答 解:设DA1交AC于点F.如图所示:
∵∠1=∠A+∠DFA,∠DFA=∠A1+∠2,
∴∠1=∠A+∠A1+∠2,
∴∠A+∠A1=∠1-∠2,
∵△A1DE是由△ADE沿直线DE折叠而得,
∴∠A=∠A1,
∴2∠A=∠1-∠2.
点评 此题主要考查了三角形内角和定理以及翻折变换的性质,遇到折叠的问题,一定要找准相等的量,结合题目所给出的条件在图形上找出之间的联系则可.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案
相关题目
5.教育部发布的统计数据显示,近年来越来越多的出国留学人员学成后选择回国发展,留学回国与出国留学人数“逆差”逐渐缩小,2014年各类留学回国人员总数为36.48万人,而2016年各类留学回国人员总数为43.25万人,如果设2014年到2016年各类留学回国人员总数的年平均增长率为x,那么根据题意可列出关于x的方程为( )
| A. | 36.48(1+x)=43.25 | B. | 36.48(1+2x)=43.25 | C. | 36.48(1+x)2=43.25 | D. | 36.48(1-x)2=43.25 |
7.下列图形中不是轴对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
4.我县七年级今年有4500名学生参加本次考试,要想了解这4500名学生的数学成绩从中抽取了500名考生的数学成绩进行统计分析,以下说法正确的是( )
| A. | 这500名考生是总体的一个样本 | B. | 每位考生是个体 | ||
| C. | 500名考生是总体 | D. | 这种调查是抽样调查 |
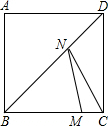 如图,正方形ABCD的边长为8,点M在BC上,且MC=2,N是BD上一动点,则NM+NC的最小值等于10.
如图,正方形ABCD的边长为8,点M在BC上,且MC=2,N是BD上一动点,则NM+NC的最小值等于10. 如图,函数y=ax+4和y=bx的图象相交于点A,则不等式bx≥ax+4的解集为x≥2.
如图,函数y=ax+4和y=bx的图象相交于点A,则不等式bx≥ax+4的解集为x≥2.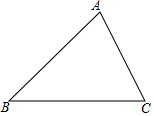 叙述三角形的中位线定理,并结合图形进行证明.
叙述三角形的中位线定理,并结合图形进行证明.