题目内容
4.设实数a是不等于1的正数,证明:下列三个方程(x-a)(x-a2)=x-a3,(x-a2)(x-a3)=x-a,(x-a3)(x-a)=x-a2中至少有两个方程存在实数根.分析 令函数y1=(x-a)(x-a2)-(x-a3)、y2=(x-a2)(x-a3)-(x-a)、y3=(x-a3)(x-a)-(x-a2),可知三个函数均为二次项系数为正的二次函数,若a>1知1<a<a2<a3,继而可得x=a2时y2<0、x=a3时y3<0,即第一、三两个方程有实数根,同理可判断0<a<1时方程的根的情况.
解答 解:设a>1,1<a<a2<a3,令函数
y1=(x-a)(x-a2)-(x-a3),
y2=(x-a2)(x-a3)-(x-a),
y3=(x-a3)(x-a)-(x-a2),
三个函数均为二次项系数为正的二次函数,
当x=a2时,y2=a-a2=a(1-a)<0,
当x=a3时,y3=a2-a3=a2(1-a)<0,
∴方程(x-a2)(x-a3)=x-a、(x-a3)(x-a)=x-a2存在实数根;
设0<a<1,0<a3<a2<a<1,
当x=a时,y1=-a+a3=a(a2-1)<0,
当x=a时,y3=-a+a2=a(a-1)<0,
∴方程(x-a)(x-a2)=x-a3、(x-a3)(x-a)=x-a2存在实数根;
综上,三个方程(x-a)(x-a2)=x-a3,(x-a2)(x-a3)=x-a,(x-a3)(x-a)=x-a2中至少有两个方程存在实数根.
点评 本题主要考查方程的根的情况,将判断一元二次方程根的情况转化为判断二次函数与x轴交点情况来求是解题的关键.

练习册系列答案
相关题目
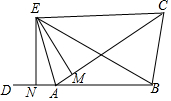 如图,在△ABC中,AC>AB,D是BA延长线上一点,点E是∠CAD平分线上一点,过点E作EM⊥AC于点M,EN⊥AD于点N,BE=CE.
如图,在△ABC中,AC>AB,D是BA延长线上一点,点E是∠CAD平分线上一点,过点E作EM⊥AC于点M,EN⊥AD于点N,BE=CE. 如图,AB是半径为1的半圆O的直径,弦CD∥AB,且$\widehat{CD}$为90°,求图中阴影部分的面积.
如图,AB是半径为1的半圆O的直径,弦CD∥AB,且$\widehat{CD}$为90°,求图中阴影部分的面积. 如图,已知五边形ABCDE中,∠A=∠B=90°,求x的度数.
如图,已知五边形ABCDE中,∠A=∠B=90°,求x的度数.