题目内容
20.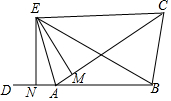 如图,在△ABC中,AC>AB,D是BA延长线上一点,点E是∠CAD平分线上一点,过点E作EM⊥AC于点M,EN⊥AD于点N,BE=CE.
如图,在△ABC中,AC>AB,D是BA延长线上一点,点E是∠CAD平分线上一点,过点E作EM⊥AC于点M,EN⊥AD于点N,BE=CE.(1)请你在不添加辅助线的情况下写出一对你认为全等的三角形,并加以证明;
(2)若AB=8,AC=10,求AM的长度.
分析 (1)在△EAN和△EAM中可利用AAS证明其全等;
(2)由条件可证明△ENB≌△EMC,可求得AC=NB,则可求得NA,结合(1)可求得AM.
解答 解:
(1)△EAN≌△EAM,
证明如下:
∵EA平分∠CAD,
∴∠EAN=∠EAM,
∵EM⊥AC,EN⊥AD,
∴∠ENA=∠EMA=90°,
在△EAN和△EAM中
$\left\{\begin{array}{l}{∠EAN=∠EAM}\\{∠ENA=∠EMA}\\{AE=AE}\end{array}\right.$
∴△EAN≌△EAM(AAS);
(2)由(1)可知EN=EM,
在Rt△△ENB和Rt△EMC中,
$\left\{\begin{array}{l}{EN=EM}\\{EB=EC}\end{array}\right.$
∴Rt△ENB≌Rt△EMC(HL),
∴AC=NB=10,
∴NA=BN-AB=10-8=2,
又由(1)可知AM=NA,
∴AM=2.
点评 本题主要考查全等三角形的判定和性质,掌握全等三角形的判定方法是解题的关键,即SSS、SAS、ASA、AAS和HL.

练习册系列答案
相关题目
10.cos30°的值是( )
| A. | $\frac{1}{2}$ | B. | 1 | C. | $\frac{\sqrt{3}}{2}$ | D. | $\frac{\sqrt{3}}{3}$ |
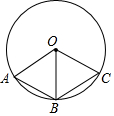 如图,OA,OB,OC是⊙O的三条半径.
如图,OA,OB,OC是⊙O的三条半径.
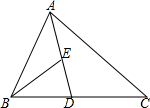 如图,AD是△ABC的中线,BE是△ABD的中线.
如图,AD是△ABC的中线,BE是△ABD的中线.