题目内容
已知抛物线y=3ax2+2bx+c,
(1)若a=b=1,c=-1,求该抛物线与x轴的交点坐标;
(2)若a+b+c=1,是否存在实数x0,使得相应的y=1?若有,请指明有几个并证明你的结论;若没有,阐述理由.
(3)若a=
,c=2+b且抛物线在-2≤x≤2区间上的最小值是-3,求b的值.
(1)若a=b=1,c=-1,求该抛物线与x轴的交点坐标;
(2)若a+b+c=1,是否存在实数x0,使得相应的y=1?若有,请指明有几个并证明你的结论;若没有,阐述理由.
(3)若a=
| 1 |
| 3 |
考点:二次函数综合题
专题:
分析:(1)先将a=b=1,c=-1代入y=3ax2+2bx+c,得到抛物线为y=3x2+2x-1,再用因式分解法求出方程3x2+2x-1=0的两个根,即可得到该抛物线与x轴的交点坐标;
(2)将y=1代入y=3ax2+2bx+c,得到3ax2+2bx+c=1,则△=4b2-12a(c-1),再将c-1=-a-b代入△,整理得到△=4[(b+
a)2+
a2],由a≠0,得出△>0,根据一元二次方程根与系数的关系可知方程3ax2+2bx+c=1有两个不相等实数根,即存在两个不同实数x0,使得相应的y=1;
(3)先将a=
,c=2+b代入y=3ax2+2bx+c,得到抛物线为y=x2+2bx+b+2,根据二次函数的性质求出其对称轴为x=-b,再分三种情况进行讨论:①x=-b<-2;②x=-b>2;③-2≤-b≤2.
(2)将y=1代入y=3ax2+2bx+c,得到3ax2+2bx+c=1,则△=4b2-12a(c-1),再将c-1=-a-b代入△,整理得到△=4[(b+
| 3 |
| 2 |
| 3 |
| 4 |
(3)先将a=
| 1 |
| 3 |
解答:解:(1)当a=b=1,c=-1时,抛物线为y=3x2+2x-1,
∵方程3x2+2x-1=0的两个根为x1=-1,x2=
,
∴该抛物线与x轴的交点坐标是(-1,0)和(
,0);
(2)存在两个不同实数x0,使得相应的y=1.理由如下:
由y=1得3ax2+2bx+c=1,即3ax2+2bx+c-1=0,
△=4b2-12a(c-1)
=4b2-12a(-a-b)
=4b2+12ab+12a2
=4(b2+3ab+3a2)
=4[(b+
a)2+
a2],
∵a≠0,
∴△>0,
所以方程3ax2+2bx+c=1有两个不相等实数根,
即存在两个不同实数x0,使得相应的y=1;
(3)若a=
,c=2+b,则抛物线可化为y=x2+2bx+b+2,其对称轴为x=-b,分三种情况:
①当x=-b<-2时,即b>2,则有抛物线在x=-2时取最小值为-3,此时-3=(-2)2+2×(-2)b+b+2,解得b=3,符合题意;
②当x=-b>2时,即b<-2,则有抛物线在x=2时取最小值为-3,此时-3=22+2×2b+b+2,解得b=-
,不合题意,舍去;
③当-2≤-b≤2时,即-2≤b≤2,则有抛物线在x=-b时取最小值为-3,此时-3=(-b)2+2×(-b)b+b+2,化简得:b2-b-5=0,解得:b=
(不合题意,舍去),b=
.
综上:b=3或b=
.
∵方程3x2+2x-1=0的两个根为x1=-1,x2=
| 1 |
| 3 |
∴该抛物线与x轴的交点坐标是(-1,0)和(
| 1 |
| 3 |
(2)存在两个不同实数x0,使得相应的y=1.理由如下:
由y=1得3ax2+2bx+c=1,即3ax2+2bx+c-1=0,
△=4b2-12a(c-1)
=4b2-12a(-a-b)
=4b2+12ab+12a2
=4(b2+3ab+3a2)
=4[(b+
| 3 |
| 2 |
| 3 |
| 4 |
∵a≠0,
∴△>0,
所以方程3ax2+2bx+c=1有两个不相等实数根,
即存在两个不同实数x0,使得相应的y=1;
(3)若a=
| 1 |
| 3 |
①当x=-b<-2时,即b>2,则有抛物线在x=-2时取最小值为-3,此时-3=(-2)2+2×(-2)b+b+2,解得b=3,符合题意;
②当x=-b>2时,即b<-2,则有抛物线在x=2时取最小值为-3,此时-3=22+2×2b+b+2,解得b=-
| 9 |
| 5 |
③当-2≤-b≤2时,即-2≤b≤2,则有抛物线在x=-b时取最小值为-3,此时-3=(-b)2+2×(-b)b+b+2,化简得:b2-b-5=0,解得:b=
1+
| ||
| 2 |
1-
| ||
| 2 |
综上:b=3或b=
1-
| ||
| 2 |
点评:本题是二次函数的综合题型,其中涉及到的知识点有二次函数的性质,抛物线与一元二次方程的关系,二次函数最值的求法.解决第(3)问时要注意分析题意分情况讨论结果.

练习册系列答案
 高效智能课时作业系列答案
高效智能课时作业系列答案
相关题目
点A(2,3)向左平移3个单位长度得到点A′,则点A′的坐标为( )
| A、(2,0) |
| B、(-1,3) |
| C、(-2,3) |
| D、(5,3) |
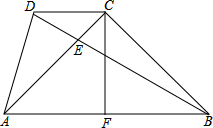 已知:如图,点C是等腰直角△ABC的直角顶点,DC∥AB,BD=AB,BD交AC于点E,CF⊥AB,垂足为F,求证:
已知:如图,点C是等腰直角△ABC的直角顶点,DC∥AB,BD=AB,BD交AC于点E,CF⊥AB,垂足为F,求证: 如图,在矩形ABCD中,AB=6,AD=10,O是BD上一点,以O为圆心作圆与AB相切于点G,
如图,在矩形ABCD中,AB=6,AD=10,O是BD上一点,以O为圆心作圆与AB相切于点G,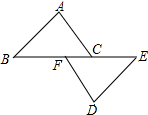 如图,点B、F、C、E在同一条直线上,FB=CE,AB∥ED,AC∥FD.
如图,点B、F、C、E在同一条直线上,FB=CE,AB∥ED,AC∥FD.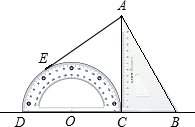 如图,将量角器和含30°角的一块直角三角板紧靠着放在同一平面内,使D,C,B在一条直线上,且DC=2BC,过点A作量角器圆弧所在圆的切线,切点为E,如果AB=6cm,则
如图,将量角器和含30°角的一块直角三角板紧靠着放在同一平面内,使D,C,B在一条直线上,且DC=2BC,过点A作量角器圆弧所在圆的切线,切点为E,如果AB=6cm,则