题目内容
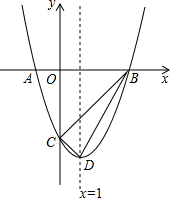 如图,在平面直角坐标系内,以直线x=1为对称轴的抛物线y=ax2+bx-3与x轴相交于A、B两点,与y轴相交于点C,点A的坐标为(-1,0).
如图,在平面直角坐标系内,以直线x=1为对称轴的抛物线y=ax2+bx-3与x轴相交于A、B两点,与y轴相交于点C,点A的坐标为(-1,0).(1)求该抛物线解析式;
(2)设该抛物线的顶点为D,连接线段BC、BD、CD,求△BCD的面积;
(3)将该抛物线向上平移,使平移后的抛物线经过原点O,且与x轴的另一个交点为E.若在y轴上存在一点F,连接DF、EF,使四边形BDFE的周长最小,求此最小值.
考点:二次函数综合题
专题:
分析:(1)由在平面直角坐标系内,以直线x=1为对称轴的抛物线y=ax2+bx-3与x轴相交于A、B两点,点A的坐标为(-1,0),可得方程组:
,解此方程组即可求得答案;
(2)首先求得点B,C,D的坐标,然后由S△BCD=S△BDM+S梯形OCDM-S△OBC,即可求得答案;
(3)首先可求得BD,BE的长,然后确定县F的位置,继而求得答案.
|
(2)首先求得点B,C,D的坐标,然后由S△BCD=S△BDM+S梯形OCDM-S△OBC,即可求得答案;
(3)首先可求得BD,BE的长,然后确定县F的位置,继而求得答案.
解答:解:(1)∵在平面直角坐标系内,以直线x=1为对称轴的抛物线y=ax2+bx-3与x轴相交于A、B两点,点A的坐标为(-1,0),
∴
,
 解得:
解得:
,
∴该抛物线解析式为:y=x2-2x-3;
(2)∵y=x2-2x-3=(x-1)2-4,
∵点D的坐标为:(1,-4),
∵令x=0,则y=-3,
∴C(0,-3),
点B与A关于直线x=1对称,
∴点B(3,0),
设直线x=1交x轴于点M,
∴OM=1,BM=3-1=2,DM=4,
∴S△BCD=S△BDM+S梯形OCDM-S△OBC=
×2×4+
×(3+4)×1-
×3×3=3;
 (3)设平移后的抛物线为:y=x2-2x-3+k,
(3)设平移后的抛物线为:y=x2-2x-3+k,
∵此抛物线过原点,
∴k=3,
∴平移后的解析式为:y=x2-2x,
∴点E(2,0),
∵四边形BDFE的周长为:BD+BE+DF+EF,
其中,BD=
=2
,BE=3-2=1,
∴要使得四边形BDFE的周长最小,只需要DF+EF取得最小值,
如图,点E关于y轴的对称点E′(-2,0),连接DE′,交y轴于点F,此时DF+EF最小,
∴DF+EF=DE′=
=5,
∴四边形BDFE的周长的最小值为:2
+1+5=6+2
.
∴
|
 解得:
解得:
|
∴该抛物线解析式为:y=x2-2x-3;
(2)∵y=x2-2x-3=(x-1)2-4,
∵点D的坐标为:(1,-4),
∵令x=0,则y=-3,
∴C(0,-3),
点B与A关于直线x=1对称,
∴点B(3,0),
设直线x=1交x轴于点M,
∴OM=1,BM=3-1=2,DM=4,
∴S△BCD=S△BDM+S梯形OCDM-S△OBC=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
 (3)设平移后的抛物线为:y=x2-2x-3+k,
(3)设平移后的抛物线为:y=x2-2x-3+k,∵此抛物线过原点,
∴k=3,
∴平移后的解析式为:y=x2-2x,
∴点E(2,0),
∵四边形BDFE的周长为:BD+BE+DF+EF,
其中,BD=
| (3-1)2+42 |
| 5 |
∴要使得四边形BDFE的周长最小,只需要DF+EF取得最小值,
如图,点E关于y轴的对称点E′(-2,0),连接DE′,交y轴于点F,此时DF+EF最小,
∴DF+EF=DE′=
| (1+2)2+42 |
∴四边形BDFE的周长的最小值为:2
| 5 |
| 5 |
点评:此题考查了待定系数法求二次函数的解析式、二次函数的性质、二次函数的平移以及周长最短问题.此题难度较大,综合性较强,注意掌握辅助线的作法,注意掌握数形结合思想与方程思想的应用.

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案
相关题目
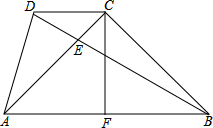 已知:如图,点C是等腰直角△ABC的直角顶点,DC∥AB,BD=AB,BD交AC于点E,CF⊥AB,垂足为F,求证:
已知:如图,点C是等腰直角△ABC的直角顶点,DC∥AB,BD=AB,BD交AC于点E,CF⊥AB,垂足为F,求证: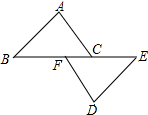 如图,点B、F、C、E在同一条直线上,FB=CE,AB∥ED,AC∥FD.
如图,点B、F、C、E在同一条直线上,FB=CE,AB∥ED,AC∥FD.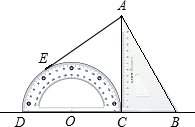 如图,将量角器和含30°角的一块直角三角板紧靠着放在同一平面内,使D,C,B在一条直线上,且DC=2BC,过点A作量角器圆弧所在圆的切线,切点为E,如果AB=6cm,则
如图,将量角器和含30°角的一块直角三角板紧靠着放在同一平面内,使D,C,B在一条直线上,且DC=2BC,过点A作量角器圆弧所在圆的切线,切点为E,如果AB=6cm,则