题目内容
 如图,在直角坐标系xOy中,直线L:y=-x-1,双曲线y=
如图,在直角坐标系xOy中,直线L:y=-x-1,双曲线y=| 1 |
| x |
考点:一次函数图象上点的坐标特征,反比例函数图象上点的坐标特征
专题:规律型
分析:根据反比例函数与一次函数图象上点的坐标特征分别求出A1、B1、A2、B2、A3、B3…,从而得到每3次变化为一个循环组依次循环,用2014除以3,根据商和余数的情况确定出a2014即可.
解答:解:∵a1=2,
∴点A1的纵坐标为-2-1=-3,
点A1(2,-3),
∵A1B1⊥x轴,点B1在双曲线y=
,
∴点B1(2,
),
∵A2B1⊥y轴,
∴点A2的纵坐标为
,
-x-1=
,
解得x=-
,
∴点A2(-
,
),
同理可求B2(-
,-
),
A3(-
,-
),B3(-
,-3),
A4(2,-3),B4(2,
),
…,
依此类推,每3次变化为一个循环组依次循环,
∵2014÷3=671余1,
∴A2014为第672循环组的第一个点,与点A1重合,
∴a2014=a1=2.
故答案为:2.
∴点A1的纵坐标为-2-1=-3,
点A1(2,-3),
∵A1B1⊥x轴,点B1在双曲线y=
| 1 |
| x |
∴点B1(2,
| 1 |
| 2 |
∵A2B1⊥y轴,
∴点A2的纵坐标为
| 1 |
| 2 |
-x-1=
| 1 |
| 2 |
解得x=-
| 3 |
| 2 |
∴点A2(-
| 3 |
| 2 |
| 1 |
| 2 |
同理可求B2(-
| 3 |
| 2 |
| 2 |
| 3 |
A3(-
| 1 |
| 3 |
| 2 |
| 3 |
| 1 |
| 3 |
A4(2,-3),B4(2,
| 1 |
| 2 |
…,
依此类推,每3次变化为一个循环组依次循环,
∵2014÷3=671余1,
∴A2014为第672循环组的第一个点,与点A1重合,
∴a2014=a1=2.
故答案为:2.
点评:本题考查了一次函数图象上点的坐标特征,反比例函数图象上点的坐标特征,依次求出各点的坐标,观察出每3次变化为一个循环组依次循环是解题的关键,也是本题的难点.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
点A(2,3)向左平移3个单位长度得到点A′,则点A′的坐标为( )
| A、(2,0) |
| B、(-1,3) |
| C、(-2,3) |
| D、(5,3) |
 如图,把长为40cm,宽30cm的长方形硬纸板,剪掉2个小正方形和2个小长方形(阴影部分即剪掉的部分),将剩余的部分拆成一个有盖的长方体盒子,设剪掉的小正方形边长为xcm(纸板的厚度忽略不计)
如图,把长为40cm,宽30cm的长方形硬纸板,剪掉2个小正方形和2个小长方形(阴影部分即剪掉的部分),将剩余的部分拆成一个有盖的长方体盒子,设剪掉的小正方形边长为xcm(纸板的厚度忽略不计)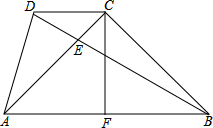 已知:如图,点C是等腰直角△ABC的直角顶点,DC∥AB,BD=AB,BD交AC于点E,CF⊥AB,垂足为F,求证:
已知:如图,点C是等腰直角△ABC的直角顶点,DC∥AB,BD=AB,BD交AC于点E,CF⊥AB,垂足为F,求证: