题目内容
15. 如图:⊙O的直径AB⊥CD于P,AP=CD=4cm,则OP=$\frac{5}{2}$cm.
如图:⊙O的直径AB⊥CD于P,AP=CD=4cm,则OP=$\frac{5}{2}$cm.
分析 连接CO,根据垂径定理可得CP=$\frac{1}{2}$CD=2cm,设OP=xcm,则CO=AO=(4-x)cm,再在Rt△COP中利用勾股定理计算即可.
解答 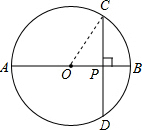 解:连接CO,
解:连接CO,
∵⊙O的直径AB⊥CD于P,
∴CP=$\frac{1}{2}$CD=2cm,
设OP=xcm,
∵AP=4cm,
∴CO=AO=(4-x)cm,
在Rt△COP中,CO2=OP2+PC2,
∴x2=(4-x)2+22,
解得:x=$\frac{5}{2}$.
∴OP=$\frac{5}{2}$cm,
故答案为:$\frac{5}{2}$.
点评 此题主要考查了垂径定理和勾股定理,关键是掌握垂直弦的直径平分这条弦,并且平分弦所对的两条弧.

练习册系列答案
 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
5.关于x的方程(m-2)x2+2x+1=0有实数根,则偶数m的最大值为( )
| A. | -2 | B. | 0 | C. | 2 | D. | 4 |
6.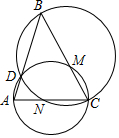 如图,在锐角△ABC中,∠ACB=60°,点D为线段AB上的一点,△ACD的外接圆交BC于点M,△BCD的外接圆交AC于点N,则$\frac{CM}{CA}$+$\frac{CN}{CB}$=( )
如图,在锐角△ABC中,∠ACB=60°,点D为线段AB上的一点,△ACD的外接圆交BC于点M,△BCD的外接圆交AC于点N,则$\frac{CM}{CA}$+$\frac{CN}{CB}$=( )
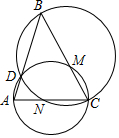 如图,在锐角△ABC中,∠ACB=60°,点D为线段AB上的一点,△ACD的外接圆交BC于点M,△BCD的外接圆交AC于点N,则$\frac{CM}{CA}$+$\frac{CN}{CB}$=( )
如图,在锐角△ABC中,∠ACB=60°,点D为线段AB上的一点,△ACD的外接圆交BC于点M,△BCD的外接圆交AC于点N,则$\frac{CM}{CA}$+$\frac{CN}{CB}$=( )| A. | 1 | B. | $\sqrt{3}$ | C. | $\frac{\sqrt{6}}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
3.15:40时,时针与分针所成角的度数是( )
| A. | 120 | B. | 130 | C. | 140 | D. | 150 |
20.在对-$\frac{3}{4}$a2x+3axy2进行因式分解时,公因式最好是( )
| A. | ax | B. | $\frac{3}{4}$ax | C. | -$\frac{3}{4}$ax | D. | -$\frac{1}{4}$ax |