题目内容
15.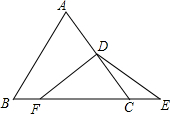 如图,△ABC是等边三角形,若D是边AC上的任意点,延长BC至E,DF=DE.请猜想AD,BF,CE之间的数量关系,并证明.
如图,△ABC是等边三角形,若D是边AC上的任意点,延长BC至E,DF=DE.请猜想AD,BF,CE之间的数量关系,并证明.
分析 作DM⊥BC于M,则∠DMC=90°,由等边三角形的性质得出AC=BC,∠ACB=60°,得出∠MDC=30°,由含30°角的直角三角形的性质得出2CD=2CM,由等腰三角形的性质得出FM=EM,即可得出结论.
解答 解:BF+CE=AD;理由如下: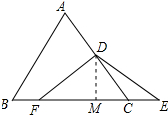
作DM⊥BC于M,则∠DMC=90°,
∵△ABC是等边三角形,
∴AC=BC,∠ACB=60°,
∴∠MDC=30°,
∴2CD=2CM,
∵DF=DE,
∴FM=EM,
∴BF+CE=BC-CF+ME-CM=AC-FM-CM+ME-CM=AC-2CM=AC-CD=AD.
点评 本题考查了等边三角形的性质、等腰三角形的性质、含30°角的直角三角形的性质;熟练掌握等边三角形的性质,通过作辅助线运用等腰三角形和直角三角形的性质是解决问题的关键.

练习册系列答案
相关题目
20.正方形ABCD中,E为BC上一点,EF⊥AC于F,EC⊥BD于G,若AC=10,那么EF+FC等于( )
| A. | 10 | B. | 5$\sqrt{2}$ | C. | 5 | D. | 2.5 |
7.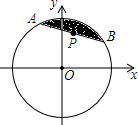 如图,圆心在原点,半径为2的圆内有一点P($\frac{\sqrt{2}}{2}$,$\frac{\sqrt{2}}{2}$),过点P作弦AB与劣弧AB组成一个弓形,则该弓形面积的最小值为( )
如图,圆心在原点,半径为2的圆内有一点P($\frac{\sqrt{2}}{2}$,$\frac{\sqrt{2}}{2}$),过点P作弦AB与劣弧AB组成一个弓形,则该弓形面积的最小值为( )
 如图,圆心在原点,半径为2的圆内有一点P($\frac{\sqrt{2}}{2}$,$\frac{\sqrt{2}}{2}$),过点P作弦AB与劣弧AB组成一个弓形,则该弓形面积的最小值为( )
如图,圆心在原点,半径为2的圆内有一点P($\frac{\sqrt{2}}{2}$,$\frac{\sqrt{2}}{2}$),过点P作弦AB与劣弧AB组成一个弓形,则该弓形面积的最小值为( )| A. | π-1 | B. | π-2 | C. | $\frac{4π}{3}$-1 | D. | $\frac{4π}{3}$-$\sqrt{3}$ |
4.把方程x2-8x-3=0化成(x+m)2=n的形式为( )
| A. | (x-8)2=3 | B. | (x-4)2=3 | C. | (x-4)2=19 | D. | (x-4)2=13 |
5.已知一元二次方程x2+0.1x-1=0的根的情况是( )
| A. | 没有实数根 | B. | 有两个相等的实数根 | ||
| C. | 有两个不相等的实数根 | D. | 无法判断 |
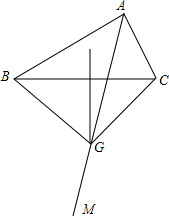 如图,已知△ABC射线AM平分∠BAC,过BC的中点作垂线,与AM相交于点G,连接BG,CG,∠BAC和∠BGC的数量关系为互补,证明你的结论.
如图,已知△ABC射线AM平分∠BAC,过BC的中点作垂线,与AM相交于点G,连接BG,CG,∠BAC和∠BGC的数量关系为互补,证明你的结论. 在由自然数排成的数阵中,在2016的正下方的自然数是多少?为什么?
在由自然数排成的数阵中,在2016的正下方的自然数是多少?为什么?