题目内容
16.不等式组$\left\{\begin{array}{l}{\frac{2x-1}{3}-\frac{5x+1}{2}≤1}\\{5x-2<3(x+2)}\end{array}\right.$的所有正整数解的和为6.分析 先求出不等式组中每个不等式的解集,然后求出其公共解集,最后求其整数解即可.
解答 解:由$\frac{2x-1}{3}$-$\frac{5x+1}{2}$≤1,得
x≥1;
由5x-2<3(x+2),得
x<4,
不等式组$\left\{\begin{array}{l}{\frac{2x-1}{3}-\frac{5x+1}{2}≤1}\\{5x-2<3(x+2)}\end{array}\right.$的解集是-1≤x<4,
不等式组$\left\{\begin{array}{l}{\frac{2x-1}{3}-\frac{5x+1}{2}≤1}\\{5x-2<3(x+2)}\end{array}\right.$的所有正整数解的和为1+2+3=6,
故答案为:6.
点评 本题考查了一元一次不等式组的解集,求不等式组的解集,应遵循以下原则:同大取较大,同小取较小,小大大小中间找,大大小小解不了.

练习册系列答案
相关题目
11.函数y=$\frac{\sqrt{x+3}}{x-5}$中自变量x的取值范围是( )
| A. | x≥-3 | B. | x≠5 | C. | x≥-3或x≠5 | D. | x≥-3且x≠5 |
6.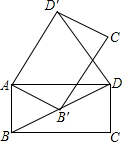 如图,在矩形ABCD中,AB=1,BC=$\sqrt{3}$.将矩形ABCD绕点A逆时针旋转至矩形AB′C′D′,使得点B′恰好落在对角线BD上,连接DD′,则DD′的长度为( )
如图,在矩形ABCD中,AB=1,BC=$\sqrt{3}$.将矩形ABCD绕点A逆时针旋转至矩形AB′C′D′,使得点B′恰好落在对角线BD上,连接DD′,则DD′的长度为( )
 如图,在矩形ABCD中,AB=1,BC=$\sqrt{3}$.将矩形ABCD绕点A逆时针旋转至矩形AB′C′D′,使得点B′恰好落在对角线BD上,连接DD′,则DD′的长度为( )
如图,在矩形ABCD中,AB=1,BC=$\sqrt{3}$.将矩形ABCD绕点A逆时针旋转至矩形AB′C′D′,使得点B′恰好落在对角线BD上,连接DD′,则DD′的长度为( )| A. | $\sqrt{3}$ | B. | $\sqrt{5}$ | C. | $\sqrt{3}$+1 | D. | 2 |
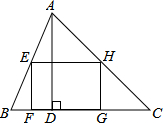 如图,矩形EFGH内接于△ABC,且边FG落在BC上.若BC=3,AD=2,EF=$\frac{2}{3}$EH,那么EH的长为$\frac{3}{2}$.
如图,矩形EFGH内接于△ABC,且边FG落在BC上.若BC=3,AD=2,EF=$\frac{2}{3}$EH,那么EH的长为$\frac{3}{2}$.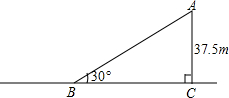 一辆汽车从斜坡顶端A处由静止开始沿斜坡滑下,速度每秒增加1.5m/s,已知斜坡高37.5m,坡角为30°.
一辆汽车从斜坡顶端A处由静止开始沿斜坡滑下,速度每秒增加1.5m/s,已知斜坡高37.5m,坡角为30°.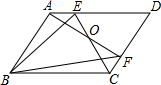 如图,在?ABCD中.E,F分别是AD,CD上,AF与CE交于点O,有下列命题:
如图,在?ABCD中.E,F分别是AD,CD上,AF与CE交于点O,有下列命题: