题目内容
6.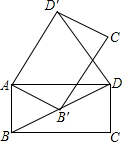 如图,在矩形ABCD中,AB=1,BC=$\sqrt{3}$.将矩形ABCD绕点A逆时针旋转至矩形AB′C′D′,使得点B′恰好落在对角线BD上,连接DD′,则DD′的长度为( )
如图,在矩形ABCD中,AB=1,BC=$\sqrt{3}$.将矩形ABCD绕点A逆时针旋转至矩形AB′C′D′,使得点B′恰好落在对角线BD上,连接DD′,则DD′的长度为( )| A. | $\sqrt{3}$ | B. | $\sqrt{5}$ | C. | $\sqrt{3}$+1 | D. | 2 |
分析 先求出∠ABD′=60°,利用旋转的性质即可得到AB=AB′,进而得到△ABB′是等边三角形,于是得到∠BAB′=60°,再次利用旋转的性质得到∠DAD′=60°,结合AD=AD′,可得到△ADD′是等边三角形,最后得到DD′的长度.
解答 解:∵矩形ABCD中,AB=1,BC=$\sqrt{3}$,
∴AD=BC=$\sqrt{3}$,
∴tan∠ABD=$\frac{AD}{AB}$=$\sqrt{3}$,
∴∠ABD=60°,
∵AB=AB′,
∴△ABB′是等边三角形,
∴∠BAB′=60°,
∴∠DAD′=60°,
∵AD=AD′,
∴△ADD′是等边三角形,
∴DD′=AD=BC=$\sqrt{3}$,
故选A.
点评 本题主要考查了旋转的性质的知识,解答本题的关键是△ABB′和△ADD′是等边三角形,此题难度不大.

练习册系列答案
相关题目
15. 如图,在平面直角坐标系中,直线AB与x轴交于点A(-2,0),与x轴夹角为30°,将△ABO沿直线AB翻折,点O的对应点C恰好落在双曲线y=$\frac{k}{x}$(k≠0)上,则k的值为( )
如图,在平面直角坐标系中,直线AB与x轴交于点A(-2,0),与x轴夹角为30°,将△ABO沿直线AB翻折,点O的对应点C恰好落在双曲线y=$\frac{k}{x}$(k≠0)上,则k的值为( )
 如图,在平面直角坐标系中,直线AB与x轴交于点A(-2,0),与x轴夹角为30°,将△ABO沿直线AB翻折,点O的对应点C恰好落在双曲线y=$\frac{k}{x}$(k≠0)上,则k的值为( )
如图,在平面直角坐标系中,直线AB与x轴交于点A(-2,0),与x轴夹角为30°,将△ABO沿直线AB翻折,点O的对应点C恰好落在双曲线y=$\frac{k}{x}$(k≠0)上,则k的值为( )| A. | 4 | B. | -2 | C. | $\sqrt{3}$ | D. | -$\sqrt{3}$ |
11.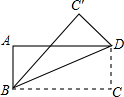 将矩形ABCD沿对角线BD折叠,使得C与C′重合,若DC′=2,则AB=( )
将矩形ABCD沿对角线BD折叠,使得C与C′重合,若DC′=2,则AB=( )
 将矩形ABCD沿对角线BD折叠,使得C与C′重合,若DC′=2,则AB=( )
将矩形ABCD沿对角线BD折叠,使得C与C′重合,若DC′=2,则AB=( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
16.下列各组中,不是同类项的是( )
| A. | 52与25 | B. | -ab与ba | C. | 0.2a2b与-$\frac{1}{5}$a2b | D. | a2b3与-a3b2 |

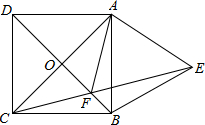 已知正方形ABCD的对角线AC,BD相交于点O,以AB为边向外作等边三角形ABE,CE与BD相交于点F,则$\frac{OA}{OF}$的值为$\sqrt{3}$.
已知正方形ABCD的对角线AC,BD相交于点O,以AB为边向外作等边三角形ABE,CE与BD相交于点F,则$\frac{OA}{OF}$的值为$\sqrt{3}$.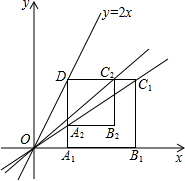 如图,在平面直角坐标系xOy中,点D为直线y=2x上且在第一象限内的任意一点,DA1⊥x轴于点A1,以DA1为边在DA1的右侧作正方形A1B1C1D;直线OC1与边DA1交于点A2,以DA2为边在DA2的右侧作正方形A2B2C2D;直线OC2与边DA1交于点A3,以DA3为边在DA3的右侧作正方形A3B3C3D,…,按这种方式进行下去,则直线OC1对应的函数表达式为y=$\frac{2}{3}$x,直线OC3对应的函数表达式为y=$\frac{14}{15}x$.
如图,在平面直角坐标系xOy中,点D为直线y=2x上且在第一象限内的任意一点,DA1⊥x轴于点A1,以DA1为边在DA1的右侧作正方形A1B1C1D;直线OC1与边DA1交于点A2,以DA2为边在DA2的右侧作正方形A2B2C2D;直线OC2与边DA1交于点A3,以DA3为边在DA3的右侧作正方形A3B3C3D,…,按这种方式进行下去,则直线OC1对应的函数表达式为y=$\frac{2}{3}$x,直线OC3对应的函数表达式为y=$\frac{14}{15}x$.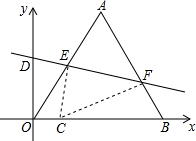 在平面直角坐标系中,等边三角形OAB的边长是2$\sqrt{3}$,且OB边落在x轴的正半轴上,点A落在第一象限.将△OAB沿直线y=kx+b折叠,使点A落在x轴上,设点C是点A落在x轴上的对应点.
在平面直角坐标系中,等边三角形OAB的边长是2$\sqrt{3}$,且OB边落在x轴的正半轴上,点A落在第一象限.将△OAB沿直线y=kx+b折叠,使点A落在x轴上,设点C是点A落在x轴上的对应点.