题目内容
4.在一个不透明的袋中装有2个黄球,3个黑球和5个红球,它们除颜色外其他都相同.(1)将袋中的球摇均匀后,求从袋中随机摸出一个球是黄球的概率;
(2)现在再将若干个红球放入袋中,与原来的10个球均匀混合在一起,使从袋中随机摸出一个球是红球的概率是$\frac{2}{3}$,请求出后来放入袋中的红球的个数.
分析 (1)用黄球的个数除以所有球的个数即可求得概率;
(2)根据概率公式列出方程求得红球的个数即可.
解答 解:(1)∵共10个球,有2个黄球,
∴P(黄球)=$\frac{2}{10}$=$\frac{1}{5}$;
(2)设有x个红球,根据题意得:$\frac{5+x}{10+x}$=$\frac{2}{3}$,
解得:x=5.
故后来放入袋中的红球有5个.
点评 此题考查了概率公式的应用.注意用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
15. 如图,在平面直角坐标系中,直线AB与x轴交于点A(-2,0),与x轴夹角为30°,将△ABO沿直线AB翻折,点O的对应点C恰好落在双曲线y=$\frac{k}{x}$(k≠0)上,则k的值为( )
如图,在平面直角坐标系中,直线AB与x轴交于点A(-2,0),与x轴夹角为30°,将△ABO沿直线AB翻折,点O的对应点C恰好落在双曲线y=$\frac{k}{x}$(k≠0)上,则k的值为( )
 如图,在平面直角坐标系中,直线AB与x轴交于点A(-2,0),与x轴夹角为30°,将△ABO沿直线AB翻折,点O的对应点C恰好落在双曲线y=$\frac{k}{x}$(k≠0)上,则k的值为( )
如图,在平面直角坐标系中,直线AB与x轴交于点A(-2,0),与x轴夹角为30°,将△ABO沿直线AB翻折,点O的对应点C恰好落在双曲线y=$\frac{k}{x}$(k≠0)上,则k的值为( )| A. | 4 | B. | -2 | C. | $\sqrt{3}$ | D. | -$\sqrt{3}$ |
12.下列各式计算正确的是( )
| A. | 5a+3a=8a2 | B. | (a-b)2=a2-b2 | C. | a3•a7=a10 | D. | (a3)2=a7 |
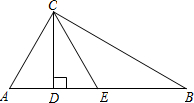 如图,已知在△ABC中,∠ACB=90°,CD为高,且CD,CE三等分∠ACB.
如图,已知在△ABC中,∠ACB=90°,CD为高,且CD,CE三等分∠ACB.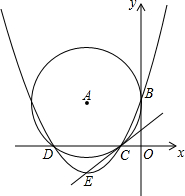 如图,在平面直角坐标系中,⊙A与x轴相交于C(-2,0),D(-8,0)两点,与y轴相切于点B(0,4).
如图,在平面直角坐标系中,⊙A与x轴相交于C(-2,0),D(-8,0)两点,与y轴相切于点B(0,4).
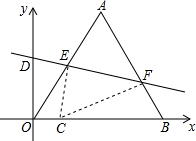 在平面直角坐标系中,等边三角形OAB的边长是2$\sqrt{3}$,且OB边落在x轴的正半轴上,点A落在第一象限.将△OAB沿直线y=kx+b折叠,使点A落在x轴上,设点C是点A落在x轴上的对应点.
在平面直角坐标系中,等边三角形OAB的边长是2$\sqrt{3}$,且OB边落在x轴的正半轴上,点A落在第一象限.将△OAB沿直线y=kx+b折叠,使点A落在x轴上,设点C是点A落在x轴上的对应点.