题目内容
6.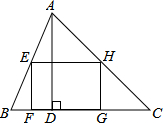 如图,矩形EFGH内接于△ABC,且边FG落在BC上.若BC=3,AD=2,EF=$\frac{2}{3}$EH,那么EH的长为$\frac{3}{2}$.
如图,矩形EFGH内接于△ABC,且边FG落在BC上.若BC=3,AD=2,EF=$\frac{2}{3}$EH,那么EH的长为$\frac{3}{2}$.
分析 设EH=3x,表示出EF,由AD-EF表示出三角形AEH的边EH上的高,根据三角形AEH与三角形ABC相似,利用相似三角形对应边上的高之比等于相似比求出x的值,即为EH的长.
解答 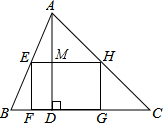 解:∵四边形EFGH是矩形,
解:∵四边形EFGH是矩形,
∴EH∥BC,
∴△AEH∽△ABC,
∵AM⊥EH,AD⊥BC,
∴$\frac{AM}{AD}$=$\frac{EH}{BC}$,
设EH=3x,则有EF=2x,AM=AD-EF=2-2x,
∴$\frac{2-2x}{2}$=$\frac{3x}{3}$,
解得:x=$\frac{1}{2}$,
则EH=$\frac{3}{2}$.
故答案为:$\frac{3}{2}$.
点评 此题考查了相似三角形的判定与性质,以及矩形的性质,熟练掌握相似三角形的判定与性质是解本题的关键.

练习册系列答案
相关题目
1. 如图,BC是⊙O的直径,点A是⊙O上异于B,C的一点,则∠A的度数为( )
如图,BC是⊙O的直径,点A是⊙O上异于B,C的一点,则∠A的度数为( )
 如图,BC是⊙O的直径,点A是⊙O上异于B,C的一点,则∠A的度数为( )
如图,BC是⊙O的直径,点A是⊙O上异于B,C的一点,则∠A的度数为( )| A. | 60° | B. | 70° | C. | 80° | D. | 90° |
11.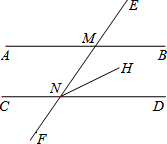 如图,已知直线AB∥CD,且直线EF分别交AB、CD于M、N两点,NH是∠MND的角平分线.若∠AMN=56°,则∠MNH的度数是( )
如图,已知直线AB∥CD,且直线EF分别交AB、CD于M、N两点,NH是∠MND的角平分线.若∠AMN=56°,则∠MNH的度数是( )
 如图,已知直线AB∥CD,且直线EF分别交AB、CD于M、N两点,NH是∠MND的角平分线.若∠AMN=56°,则∠MNH的度数是( )
如图,已知直线AB∥CD,且直线EF分别交AB、CD于M、N两点,NH是∠MND的角平分线.若∠AMN=56°,则∠MNH的度数是( )| A. | 28° | B. | 30° | C. | 34° | D. | 56° |
15. 如图,在平面直角坐标系中,直线AB与x轴交于点A(-2,0),与x轴夹角为30°,将△ABO沿直线AB翻折,点O的对应点C恰好落在双曲线y=$\frac{k}{x}$(k≠0)上,则k的值为( )
如图,在平面直角坐标系中,直线AB与x轴交于点A(-2,0),与x轴夹角为30°,将△ABO沿直线AB翻折,点O的对应点C恰好落在双曲线y=$\frac{k}{x}$(k≠0)上,则k的值为( )
 如图,在平面直角坐标系中,直线AB与x轴交于点A(-2,0),与x轴夹角为30°,将△ABO沿直线AB翻折,点O的对应点C恰好落在双曲线y=$\frac{k}{x}$(k≠0)上,则k的值为( )
如图,在平面直角坐标系中,直线AB与x轴交于点A(-2,0),与x轴夹角为30°,将△ABO沿直线AB翻折,点O的对应点C恰好落在双曲线y=$\frac{k}{x}$(k≠0)上,则k的值为( )| A. | 4 | B. | -2 | C. | $\sqrt{3}$ | D. | -$\sqrt{3}$ |
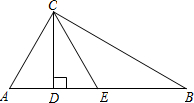 如图,已知在△ABC中,∠ACB=90°,CD为高,且CD,CE三等分∠ACB.
如图,已知在△ABC中,∠ACB=90°,CD为高,且CD,CE三等分∠ACB. 如图,已知AB是⊙O的弦,CD是⊙O的直径,CD⊥AB,垂足为E,且点E是OD的中点,⊙O的切线BM与AO的延长线相交于点M,连接AC,CM.
如图,已知AB是⊙O的弦,CD是⊙O的直径,CD⊥AB,垂足为E,且点E是OD的中点,⊙O的切线BM与AO的延长线相交于点M,连接AC,CM.