题目内容
16.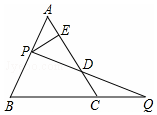 如图,过边长为1的等边△ABC的边AB上一点P,作PE⊥AC于E,Q为BC延长线一点,当PA=CQ时,连结PQ交AC于D,则DE的长为( )
如图,过边长为1的等边△ABC的边AB上一点P,作PE⊥AC于E,Q为BC延长线一点,当PA=CQ时,连结PQ交AC于D,则DE的长为( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{3}$ | D. | $\frac{2}{5}$ |
分析 过P作PF∥BC交AC于F,得出等边三角形APF,推出AP=PF=QC,根据等腰三角形性质求出EF=AE,证△PFD≌△QCD,推出FD=CD,推出DE=$\frac{1}{2}$AC即可.
解答  解:过P作PF∥BC交AC于F.如图所示:
解:过P作PF∥BC交AC于F.如图所示:
∵PF∥BC,△ABC是等边三角形,
∴∠PFD=∠QCD,△APF是等边三角形,
∴AP=PF=AF,
∵PE⊥AC,
∴AE=EF,
∵AP=PF,AP=CQ,
∴PF=CQ.
∵在△PFD和△QCD中,$\left\{\begin{array}{l}{∠PFD=∠QCD}&{\;}\\{∠PDF=∠QDC}&{\;}\\{PF=CQ}&{\;}\end{array}\right.$,
∴△PFD≌△QCD(AAS),
∴FD=CD,
∵AE=EF,
∴EF+FD=AE+CD,
∴AE+CD=DE=$\frac{1}{2}$AC,
∵AC=1,
∴DE=$\frac{1}{2}$.
故选:A.
点评 本题综合考查了全等三角形的性质和判定,等边三角形的性质和判定,等腰三角形的性质,平行线的性质等知识点的应用;证明三角形全等是解决问题的关键.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
7.下列四个数中,绝对值最大的是( )
| A. | 2 | B. | 0 | C. | -$\frac{1}{3}$ | D. | -3 |
4.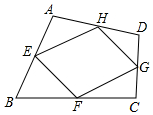 如图,四边形ABCD中,E,F,G,H分别是AB,BC,CD,AD边的中点,AC=6,BD=8,那么四边形EFGH的周长是( )
如图,四边形ABCD中,E,F,G,H分别是AB,BC,CD,AD边的中点,AC=6,BD=8,那么四边形EFGH的周长是( )
 如图,四边形ABCD中,E,F,G,H分别是AB,BC,CD,AD边的中点,AC=6,BD=8,那么四边形EFGH的周长是( )
如图,四边形ABCD中,E,F,G,H分别是AB,BC,CD,AD边的中点,AC=6,BD=8,那么四边形EFGH的周长是( )| A. | 20 | B. | 28 | ||
| C. | 14 | D. | 以上答案均有可能 |
1.某商品标价为a,若降价10%后出售,则实际售价为( )
| A. | 1.1a | B. | a | C. | 0.99a | D. | 0.9a |
5.已知线段AB,C是直线AB上的一点,AB=8,BC=4,点M是线段AC的中点,则线段AM的长为( )
| A. | 2cm | B. | 4cm | C. | 2cm或4cm | D. | 4cm或6cm |
6.如图是两个全等三角形,图中的字母表示三角形的边长,则∠1的度数是( )


| A. | 66° | B. | 60° | C. | 56° | D. | 54° |
 如图,直线AB,CD相交于O,OE平分∠AOD,∠FOC=100°,∠1=40°,求∠2和∠3的度数.
如图,直线AB,CD相交于O,OE平分∠AOD,∠FOC=100°,∠1=40°,求∠2和∠3的度数.