题目内容
5．已知线段AB，C是直线AB上的一点，AB=8，BC=4，点M是线段AC的中点，则线段AM的长为（ ）| A． | 2cm | B． | 4cm | C． | 2cm或4cm | D． | 4cm或6cm |
分析 分类讨论：点C在线段AB上，点C在线段BC的延长线上，根据线段的和差，可得AC的长，根据线段中点的性质，可得AM的长．
解答 解：①当点C在线段AB上时，由线段的和差，得AC=AB-BC=8-4=4（cm），
由线段中点的定义，得AM=$\frac{1}{2}$AC=$\frac{1}{2}$×4=2（cm）；
②点C在线段BC的延长线上，由线段的和差，得AC=AB+BC=8+4=12（cm），
由线段中点的定义，得AM=$\frac{1}{2}$AC=$\frac{1}{2}$×12=6（cm）；
故选：C．
点评 本题考查了两点间的距离，利用了线段的和差，线段中点的定义；进行分类讨论是解决问题的关键．
练习册系列答案
全优考典单元检测卷及归类总复习系列答案
品学双优卷系列答案
相关题目
15．要了解某校1500名学生的课外作业负担情况，你认为以下抽样方法中比较合理的是（ ）
| A． | 调查全体女生 | B． | 调查全体男生 | ||
| C． | 调查九年级全体学生 | D． | 调查七、八、九年级各100名学生 |
16．
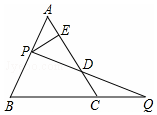如图，过边长为1的等边△ABC的边AB上一点P，作PE⊥AC于E，Q为BC延长线一点，当PA=CQ时，连结PQ交AC于D，则DE的长为（ ）
如图，过边长为1的等边△ABC的边AB上一点P，作PE⊥AC于E，Q为BC延长线一点，当PA=CQ时，连结PQ交AC于D，则DE的长为（ ）| A． | $\frac{1}{2}$ | B． | $\frac{1}{3}$ | C． | $\frac{2}{3}$ | D． | $\frac{2}{5}$ |
如图，已知∠EAC=90°，∠1+∠2=90°，∠1=∠3，DE∥BC．试说明：∠2=∠4．
20．下列图案中，不是轴对称图形的个数是（ ）
| A． | 1 | B． | 2 | C． | 3 | D． | 4 |
10．已知等腰三角形的一边长为4，另一边长为8，则它的周长是（ ）
| A． | 12 | B． | 16 | C． | 16或20 | D． | 20 |
17．以半径为1的圆的内接正三角形、正方形、正六边形的边心距（圆心到边的距离）为三边作三角形，则该三角形的面积是（ ）
| A． | $\frac{\sqrt{3}}{8}$ | B． | $\frac{\sqrt{3}}{4}$ | C． | $\frac{\sqrt{2}}{4}$ | D． | $\frac{\sqrt{2}}{8}$ |
14．下列计算正确的是（ ）
| A． | 4x2+2x2=6x4 | B． | （x-y）2=x2-y2 | C． | （x3）2=x5 | D． | x2•x2=x4 |