题目内容
7.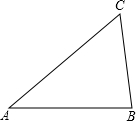 在锐角△ABC中,∠A、∠B、∠C的对边分别是a、b、c.过A作AD⊥BC于D(如图),则sinB=$\frac{AD}{c}$,sinc=$\frac{AD}{b}$,即AD=csinB,AD=bsinC,于是csinB=bsinC,即$\frac{b}{sinB}=\frac{c}{sinC}$.同理有$\frac{c}{sinC}=\frac{a}{sinA}$,$\frac{a}{sinA}=\frac{b}{sinB}$.∴$\frac{a}{sinA}=\frac{b}{sinB}=\frac{c}{sinC}$…(*)
在锐角△ABC中,∠A、∠B、∠C的对边分别是a、b、c.过A作AD⊥BC于D(如图),则sinB=$\frac{AD}{c}$,sinc=$\frac{AD}{b}$,即AD=csinB,AD=bsinC,于是csinB=bsinC,即$\frac{b}{sinB}=\frac{c}{sinC}$.同理有$\frac{c}{sinC}=\frac{a}{sinA}$,$\frac{a}{sinA}=\frac{b}{sinB}$.∴$\frac{a}{sinA}=\frac{b}{sinB}=\frac{c}{sinC}$…(*)即:在一个三角形中,各边和它所对角的正弦的比相等.
如在△ABC中,∠A=45°、∠B=60°,BC=10$\sqrt{2}$,求AC的值.
解:∵$\frac{AB}{sinA}=\frac{AC}{sinB}$,∴$\frac{{10\sqrt{2}}}{sin45°}=\frac{AC}{sin60°}\begin{array}{l}{\;}{∴AC=10\sqrt{3}}\end{array}$
(实际应用题)如图,小明要测量河内小岛C到河边公路AB的距离BC,在A点测得∠BAC=45°,在C点测得∠BCA=75°,又测得AB=60$\sqrt{3}$米,求BC的距离为多少米?(结果保留两位有效数字,参考数据$\sqrt{2}$=1.414).
分析 由阅读材料可知在一个三角形中,各边和它所对角的正弦的比相等,依此得出$\frac{BC}{sin∠BAC}$=$\frac{AB}{sin∠BCA}$,即$\frac{BC}{sin45°}$=$\frac{60\sqrt{3}}{sin75°}$,代入数据计算即可求出BC的长.
解答 解:∵$\frac{BC}{sin∠BAC}$=$\frac{AB}{sin∠BCA}$,
∴$\frac{BC}{sin45°}$=$\frac{60\sqrt{3}}{sin75°}$,
∴BC=$\frac{60\sqrt{3}×\frac{\sqrt{2}}{2}}{\frac{\sqrt{6}+\sqrt{2}}{4}}$=180-60$\sqrt{3}$≈76.
点评 本题考查了解直角三角形的应用,同时考查了学生的阅读理解能力与知识的迁移能力.理解在一个三角形中,各边和它所对角的正弦的比相等是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
18.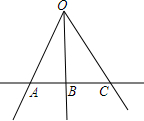 如图,下列说法正确的是( )
如图,下列说法正确的是( )
 如图,下列说法正确的是( )
如图,下列说法正确的是( )| A. | 图中共有5条线段 | B. | 直线AB与直线AC是指同一条直线 | ||
| C. | 射线AB与射线BA是指同一条射线 | D. | 点O在直线AC上 |
12.若分式$\frac{3}{(x-1)(x+2)}$有意义,则x的取值范围是( )
| A. | x≠0 | B. | x≠1且x≠-2 | C. | x≠-1或x≠-2 | D. | x=1且x=-2 |
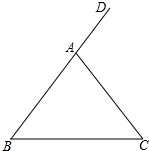 如图,△ABC中,AB=AC,∠DAC是△ABC的一个外角,
如图,△ABC中,AB=AC,∠DAC是△ABC的一个外角, 如图,△ABC中,AB=AC,以AB为直径的⊙O与BC相交于点D,与CA的延长线相交于点E,过点D作DF⊥AC于点F.
如图,△ABC中,AB=AC,以AB为直径的⊙O与BC相交于点D,与CA的延长线相交于点E,过点D作DF⊥AC于点F.