题目内容
15.先化简,再求值(1)$\frac{{{x^2}-9}}{{{x^2}+6x+9}}•\frac{{3{x^3}+9{x^2}}}{{{x^2}-3x}}$,其中x=-$\frac{1}{3}$.
(2)$\frac{x+y}{{{x^4}-{y^4}}}÷\frac{1}{{{x^2}+{y^2}}}$,其中x=8,y=11.
分析 (1)原式约分得到最简结果,把x的值代入计算即可求出值;
(2)原式利用除法法则变形,约分得到最简结果,把x与y的值代入计算即可求出值.
解答 解:(1)原式=$\frac{(x+3)(x-3)}{(x+3)^{2}}$•$\frac{3{x}^{2}(x+3)}{x(x-3)}$=3x,
当x=-$\frac{1}{3}$时,原式=-1;
(2)原式=$\frac{x+y}{(x+y)(x-y)({x}^{2}+{y}^{2})}$•(x2+y2)=$\frac{1}{x-y}$,
当x=8,y=11时,原式=-$\frac{1}{3}$.
点评 此题考查了分式的化简求值,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
5.下列语句中,正确的是( )
| A. | -$\frac{1}{3}$x=5的解是x=-$\frac{3}{5}$ | B. | 7x=-4的解是x=-$\frac{7}{4}$ | ||
| C. | -x=0的解是x=-1 | D. | $\frac{x}{-10}=0$的解是x=0 |
10.小丽的年龄乘以3再减去3是18,那么小丽现在的年龄为( )
| A. | 7岁 | B. | 8岁 | C. | 16岁 | D. | 32岁 |
20.根据下列表格对应值:
判断关于x的方程ax2+bx+c=0(a≠0)的一个解x的范围是( )
| x | -1 | 0 | 1 | 1.1 | 1.2 | 1.3 |
| ax2+bx+c | -26 | -15 | -2 | -0.59 | 0.84 | 2.29 |
| A. | x<-1 | B. | -1<x<1 | C. | 1.1<x<1.2 | D. | 1.2<x<1.3 |
4.在-$\root{3}{27}$,0,$\sqrt{9}$,0.02020020002…(每两个2之间依次多1个0),$\frac{π}{2}$,-0.33…,$\sqrt{5}$,3.1415,2.010101(每两相邻两个1之间有1个0)中,无理数有( )
| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
5.若关于的x方程x2+3x+a=0有一个根为-1,则a的值为( )
| A. | -4 | B. | -2 | C. | 2 | D. | -4 |
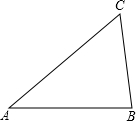 在锐角△ABC中,∠A、∠B、∠C的对边分别是a、b、c.过A作AD⊥BC于D(如图),则sinB=$\frac{AD}{c}$,sinc=$\frac{AD}{b}$,即AD=csinB,AD=bsinC,于是csinB=bsinC,即$\frac{b}{sinB}=\frac{c}{sinC}$.同理有$\frac{c}{sinC}=\frac{a}{sinA}$,$\frac{a}{sinA}=\frac{b}{sinB}$.∴$\frac{a}{sinA}=\frac{b}{sinB}=\frac{c}{sinC}$…(*)
在锐角△ABC中,∠A、∠B、∠C的对边分别是a、b、c.过A作AD⊥BC于D(如图),则sinB=$\frac{AD}{c}$,sinc=$\frac{AD}{b}$,即AD=csinB,AD=bsinC,于是csinB=bsinC,即$\frac{b}{sinB}=\frac{c}{sinC}$.同理有$\frac{c}{sinC}=\frac{a}{sinA}$,$\frac{a}{sinA}=\frac{b}{sinB}$.∴$\frac{a}{sinA}=\frac{b}{sinB}=\frac{c}{sinC}$…(*)