题目内容
16.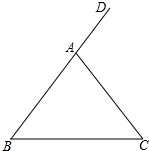 如图,△ABC中,AB=AC,∠DAC是△ABC的一个外角,
如图,△ABC中,AB=AC,∠DAC是△ABC的一个外角,实验与操作:
根据要求进行尺规作图,并在图中标明相应的字母(保留作图痕迹,不写作法)
(1)作∠DAC的平分线AM;
(2)作线段AC的垂直平分线,与AM交于点F,与BC边交于点E,连接AE;
(3)猜测AE和AF的关系,并说明理由.
分析 (1)直接利用角平分线的作法进而得出答案;
(2)利用线段垂直平分线的作法得出即可;
(3)利用全等三角形的判定得出△AEO≌△CEO(SAS),进而求出∠AEF=∠AFE,即可得出答案.
解答 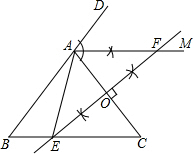 解:(1)如图所示:AM即为所求;
解:(1)如图所示:AM即为所求;
(2)如图所示:EF,AE即为所求;
(3)AE=AF,
理由:∵EF垂直平分线段AC,
∴AO=CO,
在△AEO和△CEO中,
$\left\{\begin{array}{l}{AO=CO}\\{∠AOE=∠COE}\\{EO=EO}\end{array}\right.$,
∴△AEO≌△CEO(SAS),
∴∠AEO=∠CEO,
∵∠B+∠C=∠DAC,
∠DAM=∠MAC,
∴∠MAC=∠C,
∴AM∥BC,
∴∠AFE=∠FEC,
∴∠AEF=∠AFE,
∴AE=AF.
点评 此题主要考查了复杂作图以及线段垂直平分线的性质与作法,正确把握线段垂直平分线的性质是解题关键.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目
4.在-$\root{3}{27}$,0,$\sqrt{9}$,0.02020020002…(每两个2之间依次多1个0),$\frac{π}{2}$,-0.33…,$\sqrt{5}$,3.1415,2.010101(每两相邻两个1之间有1个0)中,无理数有( )
| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
5.若关于的x方程x2+3x+a=0有一个根为-1,则a的值为( )
| A. | -4 | B. | -2 | C. | 2 | D. | -4 |
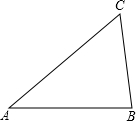 在锐角△ABC中,∠A、∠B、∠C的对边分别是a、b、c.过A作AD⊥BC于D(如图),则sinB=$\frac{AD}{c}$,sinc=$\frac{AD}{b}$,即AD=csinB,AD=bsinC,于是csinB=bsinC,即$\frac{b}{sinB}=\frac{c}{sinC}$.同理有$\frac{c}{sinC}=\frac{a}{sinA}$,$\frac{a}{sinA}=\frac{b}{sinB}$.∴$\frac{a}{sinA}=\frac{b}{sinB}=\frac{c}{sinC}$…(*)
在锐角△ABC中,∠A、∠B、∠C的对边分别是a、b、c.过A作AD⊥BC于D(如图),则sinB=$\frac{AD}{c}$,sinc=$\frac{AD}{b}$,即AD=csinB,AD=bsinC,于是csinB=bsinC,即$\frac{b}{sinB}=\frac{c}{sinC}$.同理有$\frac{c}{sinC}=\frac{a}{sinA}$,$\frac{a}{sinA}=\frac{b}{sinB}$.∴$\frac{a}{sinA}=\frac{b}{sinB}=\frac{c}{sinC}$…(*)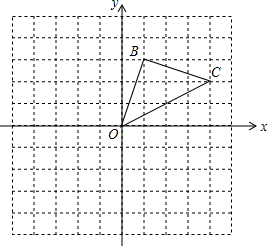 如图,在平面直角坐标系中,三角形OBC的顶点都在网格格点上,一个格是一个单位长度.
如图,在平面直角坐标系中,三角形OBC的顶点都在网格格点上,一个格是一个单位长度.